Question

In a given triangle, if we produce two straight lines, it will be $10$ triangles. Draw two lines.

Answer 1

Hint: In order to solve this question, we have to join the lines in a step-by-step manner.
Also we have to create a line and then we will count the triangles
Finally we get the required answer.

Complete step-by-step answer:
It is stated in the question we have produced straight lines in such a way that there will be $10$ triangles.
Here we have to name as the point as the given triangle as follows:

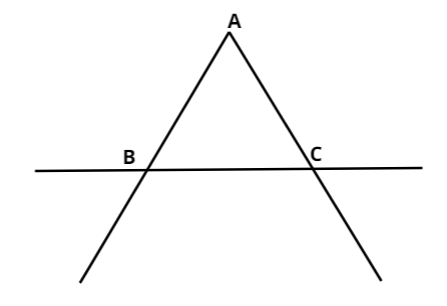
For this reason, we have to join one straight at the first instance, from the point $G$ to $E$
In the next instance we have to join one more straight line from the point $F$ to $D$.

Now let us count the total number of triangles in the resultant figure.
Thus the required triangles are $\vartriangle ACD$,$\vartriangle DFI$,$\vartriangle GCH$,$\vartriangle IJE$,$\vartriangle HDJ$,$\vartriangle ADF$, $\vartriangle FDC$,$\vartriangle GED$,$\vartriangle FJC$,$\vartriangle AHI$.
So we get $10$ triangles by drawing two lines.

Note: It is a simple question where we have to apply a simple trick of joining lines.
In geometry, a triangle can be defined as a figure which is bounded by three sides.
A triangle has three edges, three vertices and three angles.
Area of a triangle is always equal to the half of the product of base and height
The third side of the triangle is always smaller than the sum of the length of the other two sides.
On the basis of angles there are three kinds of triangles such as acute angled triangle, obtuse angled triangle and right angled triangle.
On the basis of sides of the triangle there are three types such as equilateral triangle, isosceles triangle and scalene triangle.