
In a factory, the cost of manufacturing $x$ articles is $Rs.20+2x$ and the selling price of $x$ articles is $Rs.(2.5)x$. Draw the graph and determine.
1) Number of articles to be manufactured and sold to reach break-even point (no profit and no loss situation);
2)The profit made when 60 articles are manufactured and sold.
Answer
577.2k+ views
Hint: For solving the question
1) We have to equate the cost of manufacturing$x$article = the selling price of $x$ articles.
2) We have to replace the x by 60.
For drawing the graph, we should take different values of $x$.
Complete step by step answer:
Here in this question it is given that
The cost of manufacturing $x$article is$Rs.20+2x$.
The selling price of $x$ articles is$Rs.(2.5)x$.
For the break-even point(no profit and no loss situation),
The cost of manufacturing$x$article = the selling price of $x$ articles.
$\begin{align}
& \Rightarrow Rs.20+2x=Rs.\left( 2.5 \right)x \\
& \Rightarrow 20=(2.5)x-2x \\
& \Rightarrow 20=(0.5)x \\
& \Rightarrow x=\dfrac{20}{0.5} \\
& \Rightarrow x=40
\end{align}$
For $x=40$ the break-even point occurs, that is the cost of manufacturing = the selling price.
The cost of manufacturing when 60 articles are manufactured will be
$\begin{align}
& =Rs.20+2(60) \\
& \Rightarrow Rs.20+120 \\
& \Rightarrow Rs.140 \\
\end{align}$
The money earned because of selling when 60 articles are sold will be
$\begin{align}
& \Rightarrow Rs.\left( 2.5 \right)\left( 60 \right) \\
& \Rightarrow Rs.\left( 150 \right)
\end{align}$
The profit made when 60 articles are manufactured and sold will be
\[\begin{align}
& =\text{ }\left( the\text{ }money\text{ }earned\text{ }\text{ }the\text{ }cost\text{ }of\text{ }manufacturing \right)~ \\
& =\left( Rs.150 \right)-\left( Rs.140 \right) \\
& \Rightarrow Rs.10 \\
\end{align}\]
The profit made when 60 articles are manufactured and sold = Rs.10
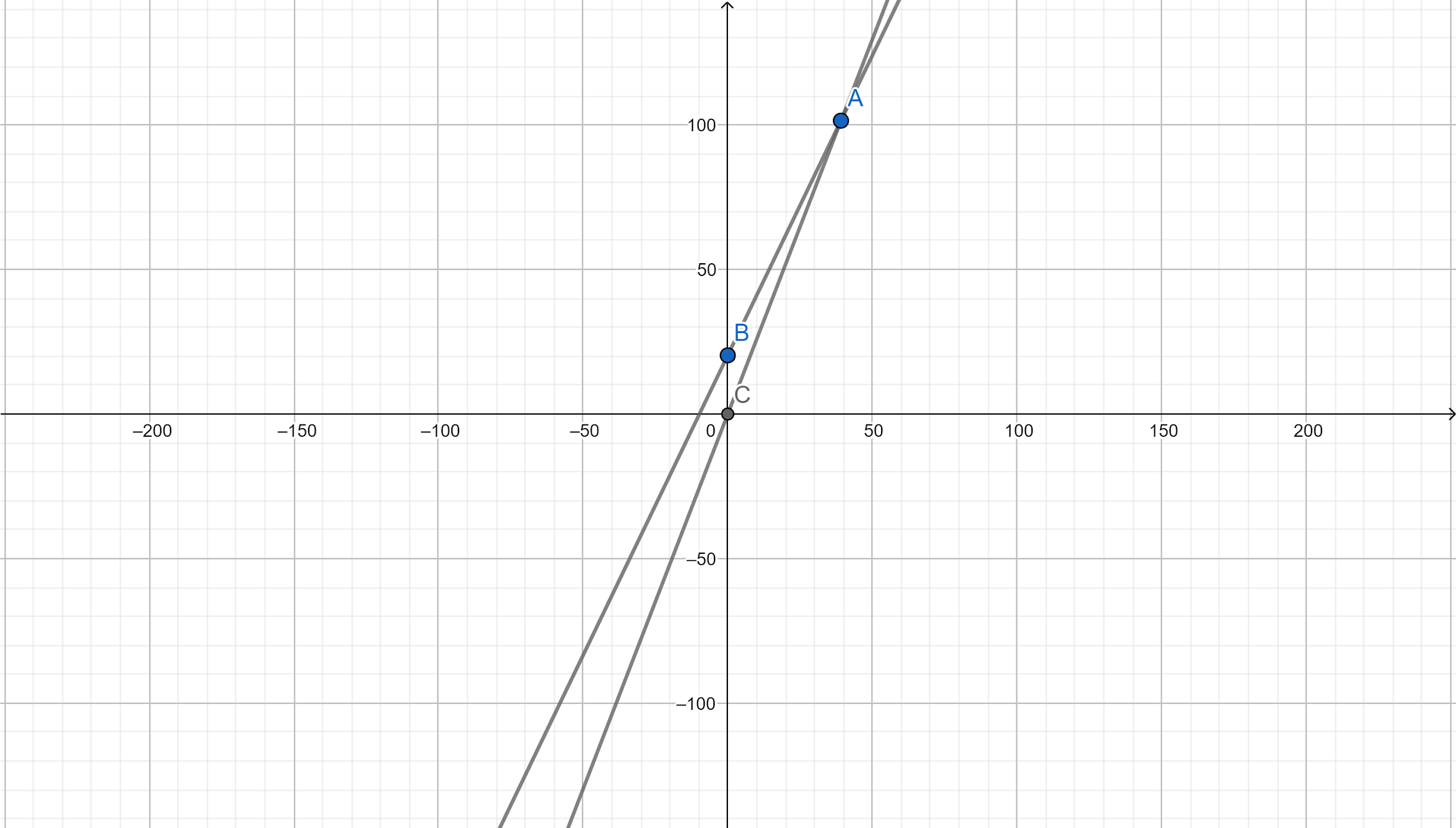
For drawing the graph,
For the line of cost of manufacturing $Rs.20+2x$
For the line of money earned by selling the articles $Rs.(2.5)x$
.
Note: While solving this question we should take care that the profit occurs only when the cost of manufacturing is less than the money earned by selling the articles and when the cost of manufacturing is greater than the money earned by selling the articles, the loss occurs.
1) We have to equate the cost of manufacturing$x$article = the selling price of $x$ articles.
2) We have to replace the x by 60.
For drawing the graph, we should take different values of $x$.
Complete step by step answer:
Here in this question it is given that
The cost of manufacturing $x$article is$Rs.20+2x$.
The selling price of $x$ articles is$Rs.(2.5)x$.
For the break-even point(no profit and no loss situation),
The cost of manufacturing$x$article = the selling price of $x$ articles.
$\begin{align}
& \Rightarrow Rs.20+2x=Rs.\left( 2.5 \right)x \\
& \Rightarrow 20=(2.5)x-2x \\
& \Rightarrow 20=(0.5)x \\
& \Rightarrow x=\dfrac{20}{0.5} \\
& \Rightarrow x=40
\end{align}$
For $x=40$ the break-even point occurs, that is the cost of manufacturing = the selling price.
The cost of manufacturing when 60 articles are manufactured will be
$\begin{align}
& =Rs.20+2(60) \\
& \Rightarrow Rs.20+120 \\
& \Rightarrow Rs.140 \\
\end{align}$
The money earned because of selling when 60 articles are sold will be
$\begin{align}
& \Rightarrow Rs.\left( 2.5 \right)\left( 60 \right) \\
& \Rightarrow Rs.\left( 150 \right)
\end{align}$
The profit made when 60 articles are manufactured and sold will be
\[\begin{align}
& =\text{ }\left( the\text{ }money\text{ }earned\text{ }\text{ }the\text{ }cost\text{ }of\text{ }manufacturing \right)~ \\
& =\left( Rs.150 \right)-\left( Rs.140 \right) \\
& \Rightarrow Rs.10 \\
\end{align}\]
The profit made when 60 articles are manufactured and sold = Rs.10
For drawing the graph,
For the line of cost of manufacturing $Rs.20+2x$
| X | $Rs.20+2x$ |
| 0 | 20 |
| 40 | 100 |
| 60 | 140 |
For the line of money earned by selling the articles $Rs.(2.5)x$
| X | $Rs.(2.5)x$ |
| 0 | 0 |
| 40 | 100 |
.

Note: While solving this question we should take care that the profit occurs only when the cost of manufacturing is less than the money earned by selling the articles and when the cost of manufacturing is greater than the money earned by selling the articles, the loss occurs.
Recently Updated Pages
The stick and ball games played in England some 500 class 9 social science CBSE

The curved surface area of a frustum cone is 25pi mm2 class 9 maths CBSE

The cost of painting the curved surface area of a cone class 9 maths CBSE

Prove that the equation x2 + px 1 0 has real and distinct class 9 maths CBSE

What is the name of a parallelogram with all sides class 9 maths CBSE

If a b are coprime then a2b2 are a Coprime b Not coprime class 9 maths CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Which places in India experience sunrise first and class 9 social science CBSE

Name 10 Living and Non living things class 9 biology CBSE

What is the full form of pH?

Write the 6 fundamental rights of India and explain in detail




