Question

In a \[\Delta ABC,\text{ }{{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C=1\]. Prove that the triangle is right-angled.

Answer 1

Hint: Assume a right-angled triangle ABC. Take the cos of each angle of \[\Delta ABC\] and square them separately. Add them to get \[{{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C=1\]. Since we are already given this result, this means that our assumption is correct. Hence solve the question by this approach.

Complete step-by-step answer:
Here we are given that in \[\Delta ABC,\text{ }{{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C=1\]. We have to prove that triangle ABC is a right-angled triangle.
Let us assume a \[\Delta ABC\] such that it is right-angled at B.

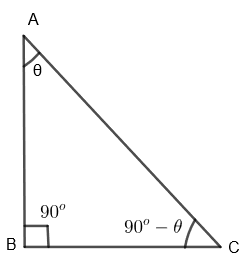
Let us take \[\angle A=\theta \], we know that in any triangle, the sum of 3 angles is \[{{180}^{o}}\]. So, we get,
\[\angle A+\angle B+\angle C={{180}^{o}}\]
By substituting the value of \[\angle A=\theta \] and \[\angle B={{90}^{o}}\], we get,
\[\theta +{{90}^{o}}+\angle C={{180}^{o}}\]
$\Rightarrow$ \[\angle C={{180}^{o}}-\theta -{{90}^{o}}\]
$\Rightarrow$ \[\angle C={{90}^{o}}-\theta \]
Now, we know that \[\angle A=\theta \]. By taking cos on both sides, of the above equation, we get,
\[\cos \left( A \right)=\cos \theta \]
By squaring both sides of the above equation, we get
$\Rightarrow$ \[{{\cos }^{2}}\left( A \right)={{\cos }^{2}}\theta ....\left( i \right)\]
Now, we also know that \[\angle B={{90}^{o}}\].
By taking cos on both sides of the above equation, we get
$\Rightarrow$ \[\cos B=\cos {{90}^{o}}\]
By squaring both sides of the above equation, we get,
$\Rightarrow$ \[{{\cos }^{2}}B={{\cos }^{2}}{{90}^{o}}\]
We know that \[\cos {{90}^{o}}=0\], so we get,
$\Rightarrow$ \[{{\cos }^{2}}B=0....\left( ii \right)\]
Now, we have found that \[\angle C=\left( {{90}^{o}}-\theta \right)\]
By taking cos on both sides of the above equation, we get,
$\Rightarrow$ \[\cos C=\cos \left( 90-\theta \right)\]
By squaring both sides of the above equation, we get,
$\Rightarrow$ \[{{\cos }^{2}}C={{\cos }^{2}}\left( 90-\theta \right)\]
We know that \[\cos \left( 90-\theta \right)=\sin \theta \]. So, we get,
$\Rightarrow$ \[{{\cos }^{2}}C={{\sin }^{2}}\theta ....\left( iii \right)\]
By adding equation (i), (ii) and (iii), we get,
$\Rightarrow$ \[{{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C={{\cos }^{2}}\theta +0+{{\sin }^{2}}\theta \]
$\Rightarrow$ \[{{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C={{\cos }^{2}}\theta +{{\sin }^{2}}\theta \]
We know that \[{{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1\]. So, we get,
$\Rightarrow$ \[{{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C=1\]
This result is the same as what is given in the question and this is true only for our assumption. That means our assumption was correct. Therefore, we get \[\Delta ABC\] as a right-angled triangle.
Hence proved.

Note: In these types of questions, students are advised to go in the reverse direction. That means, they must assume the desired result and solve accordingly to prove the result already given in the question. If they can finally get the result already given in the question that means their assumption was correct.