Question

In a certain town, 25% of the families own a phone and 15% own a car, 65% of families own neither a phone nor a car and 2000 families own both a car and a phone. Consider following three statements:
(a) 5% of the families own both a car and a phone.
(b) 35% of the families own either a car and a phone.
(c) 40,000 families live in the town.
Then,
A. All (a), (b) and (c) are correct.
B. Only (b) and (c) are correct.
C. Only (a) and (b) are correct.
D. Only (a) and (c) are correct.

Answer 1

Hint: Here using the information we draw a Venn diagram and assume the number of people living in the town as a variable and calculate each percentage in terms of fraction. We denote each value in terms of probability of set and using the formula for set union find the values.
* Set theory formula of number of elements in the union of 2 sets : \[n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\]

Complete step-by-step answer:
We draw a Venn diagram of the question
               

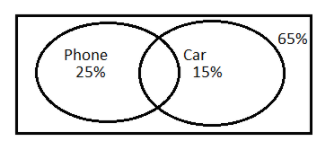
Step 1: Solving for option (c)
Let x be the number of families living in the town.
P denotes families owning a phone.
C denotes families owning a car.
So families owning both a phone and car will be denoted by \[P \cap C\].
Now we convert percentage into fraction form.
Number of families owning a phone is \[25\% \] of \[x\].
\[
   \Rightarrow n(P) = \dfrac{{25}}{{100}}x \\
   \Rightarrow n(P) = \dfrac{x}{4} \\
 \]
Number of families owning a car is \[15\% \] of \[x\].
$
   \Rightarrow n(C) = \dfrac{{15}}{{100}}x \\
   \Rightarrow n(C) = \dfrac{{3x}}{{20}} \\
 $
We are given a total number of families owning both a car and phone is 2000.
$ \Rightarrow n(P \cap C) = 2000$
So, number of families owning neither car nor phone will be total number of families owning car or phone subtracted from total number of families
Thus \[n\](Neither Phone nor Car)$ = x - n(P \cup C)$
Number of families owning neither a car nor a phone is \[65\% \]of \[x\].
$ \Rightarrow \dfrac{{65}}{{100}}x = x - n(P \cup C)$
Shifting all the values except $n(P \cup C)$ to one side of the equation.
$ \Rightarrow n(P \cup C) = x - \dfrac{{65x}}{{100}}$
Take LCM on the right hand side of the equation.
$
   \Rightarrow n(P \cup C) = \dfrac{{100x - 65x}}{{100}} \\
   \Rightarrow n(P \cup C) = \dfrac{{35x}}{{100}} \\
 $
Cancelling out factors we get.
$ \Rightarrow n(P \cup C) = \dfrac{{7x}}{{20}}$ … (i)
Now using the set formula we find the value of x.
Substitute the values \[n(P) = \dfrac{x}{4},n(C) = \dfrac{{3x}}{{20}}, n(P \cap C) = 2000, n(P \cup C) = \dfrac{{7x}}{{20}}\] in the formula \[n(P \cup C) = n(P) + n(C) - n(P \cap C)\] .
$ \Rightarrow \dfrac{{7x}}{{20}} = \dfrac{x}{4} + \dfrac{{3x}}{{20}} - 2000$
Taking LCM on the right hand side of the equation, only values along with the variable x.
$
   \Rightarrow \dfrac{{7x}}{{20}} = \dfrac{{5x + 3x}}{{20}} - 2000 \\
   \Rightarrow \dfrac{{7x}}{{20}} = \dfrac{{8x}}{{20}} - 2000 \\
 $
Shift all values along with variable x to one side.
$ \Rightarrow 2000 = \dfrac{{8x}}{{20}} - \dfrac{{7x}}{{20}}$
Take LCM on the right hand side of the equation.
$
   \Rightarrow 2000 = \dfrac{{8x - 7x}}{{20}} \\
   \Rightarrow 2000 = \dfrac{x}{{20}} \\
 $
Multiply both sides of the equations by 20
$
   \Rightarrow 2000 \times 20 = \dfrac{x}{{20}} \times 20 \\
   \Rightarrow 40000 = x \\
 $
Thus \[x = 40000\]. Total number of families living in town is 40000
So, option (c) is correct.
Step 2: Checking for option (a)
Now we calculate \[5\% \] of the total number of families which gives us the number of families owning both a car and a phone.
\[5\% x = \dfrac{5}{{100}} \times 40000 = 2000\]
$n(P \cap C) = 2000$ which is \[5\% \] of \[40000\].
So, option (a) is correct.
Step 3: Checking for option (b)
Now we calculate \[35\% \] of the total number of families which gives us the number of families owning either a car or a phone.
\[35\% x = \dfrac{{35}}{{100}} \times 40000 = 14000\]
$n(P \cup C) = 14,000$ which is \[35\% \]of \[40000\]
So, option (b) is correct.
Therefore, All (a), (b) and (c) are correct.

So, the correct answer is “Option A”.

Note: Students many times make the mistake of assuming the neither nor value as the value for union but they should keep in mind that neither a car nor a phone means families which have none of the items, so we subtract families having either car or phone from the total number of families. That is represented by the empty space outside the circles in the Venn diagram.