Question

If the tangent at \[\left( 1,7 \right)\] to the curve \[{{x}^{2}}=y-6\] touches the circle \[{{x}^{2}}+{{y}^{2}}+16x+12y+c=0\] then the value of \[c\] is
(a) \[85\]
(b) \[95\]
(c) \[195\]
(d) \[185\]

Answer 1

Hint: Write the equation of tangent at point \[\left( 1,7 \right)\] to the curve \[{{x}^{2}}=y-6\] using point slope form by writing the slope in terms of \[\dfrac{dy}{dx}\]. Assume a point on the circle at which the tangent touches the circle and write the slope of the line joining the centre of the circle to this point. This line is perpendicular to the tangent and thus, the product of their slopes is \[-1\]. Use this fact to find the point at which tangent touches the circle. Substitute the value of this point in the equation of the circle to find the value of \[c\].

Complete step-by-step answer:
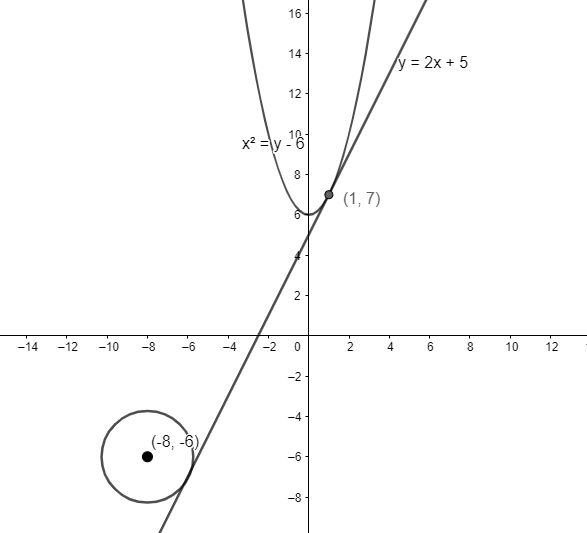
We have a curve of the form \[{{x}^{2}}=y-6\] to which tangent is drawn at point \[\left( 1,7 \right)\]. This tangent also touches the circle \[{{x}^{2}}+{{y}^{2}}+16x+12y+c=0\]. We have to find the value of parameter \[c\].

We will first find the equation of tangent to the curve \[{{x}^{2}}=y-6\] at point \[\left( 1,7 \right)\]. We can write the slope of the curve as \[\dfrac{dy}{dx}\]. Thus, differentiating the equation \[{{x}^{2}}=y-6\] on both sides, we have \[2xdx=dy\] as the derivative of any function of the form \[y=a{{x}^{n}}+b\] is \[\dfrac{dy}{dx}=an{{x}^{n-1}}\].

Thus, we have \[\dfrac{dy}{dx}=2x\]. Substituting the point \[\left( 1,7 \right)\] in the equation, we have \[\dfrac{dy}{dx}=2\] as the slope of the tangent at point \[\left( 1,7 \right)\].

We will write the equation of tangent. We know that any line passing through point \[\left( {{x}_{1}},{{y}_{1}} \right)\] having slope \[m\] is \[y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)\].

Substituting \[{{x}_{1}}=1,{{y}_{1}}=7,m=2\] in the above equation, we have \[y-7=2\left( x-1 \right)\Rightarrow y=2x+5\] as the equation of line passing through \[\left( 1,7 \right)\] having slope \[2\].

The tangent with equation \[y=2x+5\] is also tangent to the circle \[{{x}^{2}}+{{y}^{2}}+16x+12y+c=0\].

Let’s assume that tangent touches the circle at point \[\left( u,v \right)\].

Thus, the line joining centre of the circle to point \[\left( u,v \right)\] is perpendicular to the equation of tangent \[y=2x+5\].

We know that a circle with equation \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] has centre at point \[\left( -g,-f \right)\]. Thus, the centre of the circle \[{{x}^{2}}+{{y}^{2}}+16x+12y+c=0\] is \[\left( -8,-6 \right)\].

We will find the slope of the line joining the centre of the circle \[\left( -8,-6 \right)\] to the point \[\left( u,v \right)\].

We know that the slope of line joining two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is \[\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\].

Substituting \[{{x}_{1}}=-8,{{y}_{1}}=-6,{{x}_{2}}=u,{{y}_{2}}=v\] in the above equation, we have \[\dfrac{v+6}{u+8}\] as the slope of line joining the centre of circle \[\left( -8,-6 \right)\] to the point \[\left( u,v \right)\]. We know this line is perpendicular to the equation of tangent.

We know that the product of slopes of two perpendicular lines is \[-1\].

As the slope of the tangent is \[2\], we have \[\dfrac{v+6}{u+8}\left( 2 \right)=-1\].

Simplifying the above equation, we have \[2v+12=-u-8\].

\[\Rightarrow 2v+u+20=0.....\left( 1 \right)\]

We know that the point \[\left( u,v \right)\] passes through the equation of tangent \[y=2x+5\]. Thus, we have \[v=2u+5.....\left( 2 \right)\].

Substituting equation \[\left( 2 \right)\] in equation \[\left( 1 \right)\], we have \[4u+10+u+20=0\].

\[\begin{align}

  & \Rightarrow 5u+30=0 \\

 & \Rightarrow u=-6 \\

\end{align}\]

Substituting the value \[u=-6\] in equation \[\left( 1 \right)\], we have \[2v-6+20=0\].

\[\begin{align}

  & \Rightarrow 2v+14=0 \\

 & \Rightarrow v=-7 \\

\end{align}\]

Thus, we have \[\left( u,v \right)=\left( -6,-7 \right)\] as the coordinates of the point at which the tangent touches the circle. Substituting this point \[\left( u,v \right)=\left( -6,-7 \right)\] in the equation of circle \[{{x}^{2}}+{{y}^{2}}+16x+12y+c=0\], we have \[{{\left( -6 \right)}^{2}}+{{\left( -7 \right)}^{2}}+16\left( -6 \right)+12\left( -7 \right)+c=0\].

Simplifying the equation, we have \[-95+c=0\].

\[\Rightarrow c=95\]

Hence, the value of \[c\] for which the tangent to the parabola is tangent to the circle as well is \[c=95\] which is option (b).

Note: We can also solve this question by finding the foot of perpendicular drawn from the centre of the circle to the equation of tangent and then substituting the value of foot of perpendicular in the equation of circle to get the exact equation of circle.