Question

If the corresponding angles of two triangles are equal then they are always congruent. The Given statement
( a ) is always true
( b ) is always false
( c ) can be true
( d ) can be determined

Answer 1

Hint: To solve this question we will see what are the basic requirements for two triangles to be called similar or congruent and on that basis we will judge whether the statement given in the question is true or not.

Complete step-by-step answer:

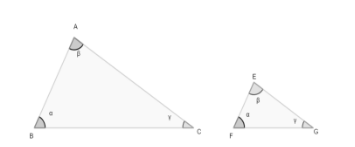
In question, it is asked that if there are two triangles and their corresponding angles are equal, then these triangles will be congruent or not.
Now, let us first see the difference between congruence and similarity of triangles.
Two triangles are said to be congruent if they both are identical in shape, size and measure, that is if we have two triangles, then if their sides are in ratio of 1:1, there all three angles are same then triangles are congruent.
Two triangles are said to be similar if they both are in the same shape and same measure but not have similar size, that is, two triangles are said to be similar if all three corresponding sides are in the same ratio, say m:n and angle measure are the same but size may be different.
Now, the question is that if corresponding angles are equal then those two triangles will be congruent or not.
Answers may be true for congruence but always true for similarity. The reason is simple that two triangles have equal corresponding angles but size is not mentioned here and corresponding angles are equal and satisfies all the conditions of similarity but not of congruence as by definition of congruence, shapes must be identical.
 $ \text{In figure, }\vartriangle \text{ABC and }\vartriangle \text{EFG}$ are similar triangles with same
So, the correct answer is “Option C”.

Note: These questions are theoretical and this needs deep knowledge of chapter. So, one must know all the properties, theorems and statements on similarity and congruence of two triangles. Always use counter examples wherever you need to disprove something if possible.