Question

If PAB is a secant to a circle of Centre O intersecting the circle of A and B and PT is tangent segment, then prove that-
${\text{PA}} \times {\text{PB = P}}{{\text{T}}^2}$

Answer 1

Hint – In this question first make a circle then draw a tangent and a secant from an external point of the circle and also, draw a perpendicular line from the Centre of the circle to the secant, then apply Pythagoras theorem .

Complete step-by-step solution -

Given Data, PAB is a secant, Centre of circle O, PT is a tangent
We make a construction that is OM ⊥ AB, OA, OP, OT, Ob are joined.

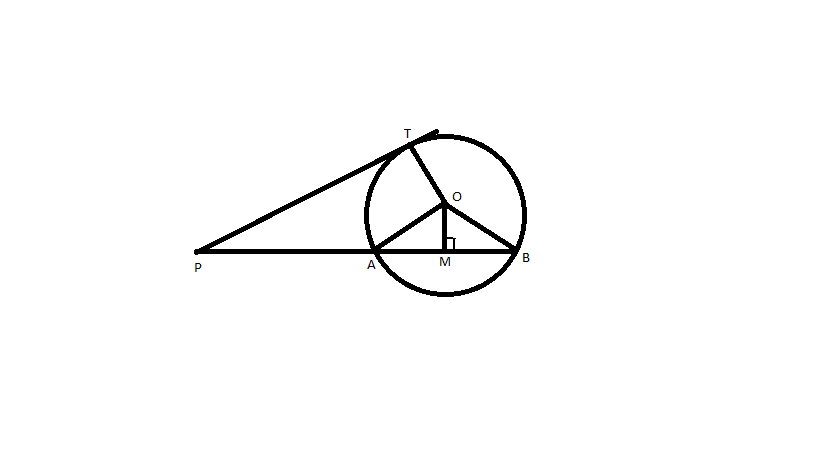
Here PAB is secant intersecting the circle with Centre O at A and B and a tangent PT at T.
Now PA = PM – AM
PB = PM + MB
As we know AM = BM (perpendicular drawn from the Centre of the circle to a chord is also a bisector of chord)
PA.PB = (PM – AM) × (PM + AM) = ${\text{P}}{{\text{M}}^2} - {\text{A}}{{\text{M}}^2}{\text{ }} \to {\text{ Equation 1}}$
Also from the diagram OM ⊥ AB
We can apply Pythagoras theorem in ∆OMP
${\text{P}}{{\text{M}}^2} = {\text{O}}{{\text{P}}^2} - {\text{O}}{{\text{M}}^2}$
We can apply Pythagoras theorem in ∆OMA
${\text{A}}{{\text{M}}^2} = {\text{O}}{{\text{A}}^2} - {\text{O}}{{\text{M}}^2}$
Put these values in Equation 1, we get
PA.PB = ${\text{P}}{{\text{M}}^2} - {\text{A}}{{\text{M}}^2}$
PA.PB = (${\text{O}}{{\text{P}}^2} - {\text{O}}{{\text{M}}^2}$) – (${\text{O}}{{\text{A}}^2} - {\text{O}}{{\text{M}}^2}$)
PA.PB = ${\text{O}}{{\text{P}}^2} - {\text{O}}{{\text{A}}^2}$
As OA = OT (radii)
PA.PB = ${\text{O}}{{\text{P}}^2} - {\text{O}}{{\text{T}}^2}{\text{ }} \to {\text{ Equation 2}}$
As radius is perpendicular to the tangent so this will form a right angled triangle, we can apply Pythagoras theorem in ∆OPT
We get ${\text{P}}{{\text{T}}^2}{\text{ = O}}{{\text{P}}^2} - {\text{O}}{{\text{T}}^2}$
By putting this in the Equation 2, we get
PA.PB = ${\text{P}}{{\text{T}}^2}$
Hence Proved.

Note – In order to solve this type of questions, draw an appropriate figure and construct any other additional elements using known geometrical properties. Pythagoras theorem can be used if we construct a right angled triangle. Properties of straight lines are very important in order to approach the answer or proof.