Question

If O is the origin and OP and OQ are the tangents from the origin to the circle $ {{x}^{2}}+{{y}^{2}}-6x+4y+8=0 $ , then the circumcentre of $ \Delta OPQ $ is
A. $ \left( 3,-2 \right) $
B. $ \left( \dfrac{3}{2},-1 \right) $
C. $ \left( \dfrac{3}{4},\dfrac{-1}{2} \right) $
D. $ \left( \dfrac{-3}{2},1 \right) $

Answer 1

Hint: We first try to form the given circle in its general form of $ {{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}} $ to find the centre and the radius. Then we try to find the circumcircle of the $ \Delta OPQ $ . We prove that it’s a cyclic quadrilateral. We find the arc creator as the diameter of the new circle. We find the midpoint of that diameter to find the solution to the problem.

Complete step by step answer:
It’s given that O is the origin and OP and OQ are the tangents from the origin to the circle $ {{x}^{2}}+{{y}^{2}}-6x+4y+8=0 $ . We transform it as $ {{\left( x-3 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=5 $ . O is the origin.
Equating with the general equation of circle $ {{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}} $ , we get the centre as $ C\equiv \left( 3,-2 \right) $ and the radius as $ \sqrt{5} $ units.

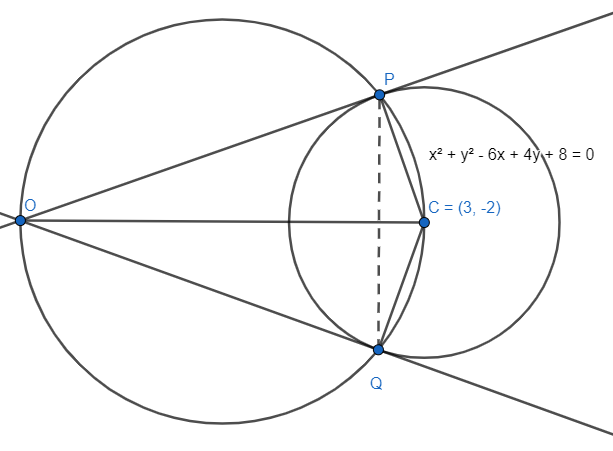
PQ is the chord of contact. So, OPCQ becomes cyclic quadrilateral.
We can see CP and CQ are radii. OP and OQ are tangents which means $ \angle OPC=\angle OQC={{90}^{\circ }} $ . The circumcircle of $ \Delta OPQ $ will intersect point C also.
Basically, the segment OC becomes the arc creator of the circumcircle as it creates the right angle at points P and Q. We can define the OC segment as the diameter of the circle.
The middle point of the points O and C becomes the circumcentre of $ \Delta OPQ $ .
The points are $ O\equiv \left( 0,0 \right) $ and $ C\equiv \left( 3,-2 \right) $ .
The middle point which is circumcentre of $ \Delta OPQ $ will be \[\left( \dfrac{3+0}{2},\dfrac{-2+0}{2} \right)\equiv \left( \dfrac{3}{2},-1 \right)\].
The correct option is B.

Note:
We also can use the general form to find the circumcentre where the centre is always \[\left( \dfrac{-g}{2},\dfrac{-f}{2} \right)\] for the circle $ {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 $ .We can sue the formula for only cyclic quadrilaterals.