Question

If O is any point in the interior of a rectangle ABCD. Prove that $O{A^2} + O{C^2} = O{B^2} + O{D^2}$. Hence find the length of OD, if the lengths of OA, OB and OC are 3 cm, 4 cm and 5 cm respectively.

Answer 1

Hint:Analyze the situation with a diagram. Take a random point O inside the square and join it with every vertex. Draw two lines passing through O and parallel to the sides AB and BC respectively. Consider four right angled triangles each to determine the values of OA, OB, OC and OD respectively in terms of some variables. Then verify the result $O{A^2} + O{C^2} = O{B^2} + O{D^2}$.

Complete step by step answer:
According to the question, a rectangle ABCD is said to have any interior point O. We have to prove that $O{A^2} + O{C^2} = O{B^2} + O{D^2}$.
Consider the rectangle ABCD shown below with a point O lying inside it.

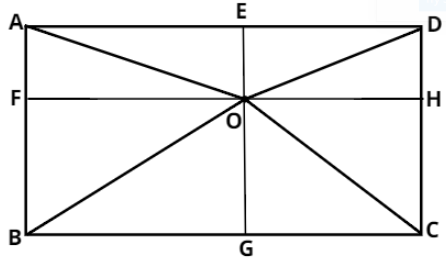
OA, OB, OC and OD are the lines joining the vertex of the square and point O. We have also drawn EG and FH parallel to the sides of the square and passing through point O.
From this we can conclude that AD, FH and BC are parallel and equal. Similarly AB, EG and DC are also parallel and equal.
So let $AF = OE = DH = a$.
Similarly we will assume some variable for other sides also as shown below:
$
   \Rightarrow FB = OG = HC = b \\
   \Rightarrow AE = OF = BG = c \\
   \Rightarrow ED = OH = GC = d \\
 $
To find the values of OA, OB, OC and OD, we’ll consider right angled triangles.
So in right angled triangle $AOF$, we have:
$ \Rightarrow O{A^2} = O{F^2} + A{F^2} = {c^2} + {a^2}{\text{ }}.....{\text{(1)}}$
Similarly in triangle $BOG$, we have:
$ \Rightarrow O{B^2} = O{G^2} + B{G^2} = {b^2} + {c^2}{\text{ }}.....{\text{(2)}}$
In triangle $COH$, we have:
$ \Rightarrow O{C^2} = O{H^2} + H{C^2} = {d^2} + {b^2}{\text{ }}.....{\text{(3)}}$
And in triangle $DOE$, we have:
$ \Rightarrow O{D^2} = O{E^2} + E{D^2} = {a^2} + {d^2}{\text{ }}.....{\text{(4)}}$
Now adding equation (1) and (3), we’ll get:
$
   \Rightarrow O{A^2} + O{C^2} = {c^2} + {a^2} + {d^2} + {b^2} \\
   \Rightarrow O{A^2} + O{C^2} = {a^2} + {b^2} + {c^2} + {d^2}{\text{ }}.....{\text{(5)}} \\
 $
And adding equation (2) and (4), we’ll get:
$
   \Rightarrow O{B^2} + O{D^2} = {b^2} + {c^2} + {a^2} + {d^2} \\
   \Rightarrow O{B^2} + O{D^2} = {a^2} + {b^2} + {c^2} + {d^2}{\text{ }}.....{\text{(6)}} \\
 $
On comparing equation (5) and (6), we can say that:
$ \Rightarrow O{A^2} + O{C^2} = O{B^2} + O{D^2}$
Hence this is proved.
Further we have to calculate the length of OD such that OA, OB and OC are 3 cm, 4 cm and 5 cm respectively.
So using the same result:
$ \Rightarrow O{A^2} + O{C^2} = O{B^2} + O{D^2}$
Putting the values, we’ll get:
$
   \Rightarrow {3^2} + {5^2} = {4^2} + O{D^2} \\
   \Rightarrow 16 + O{D^2} = 9 + 25 = 34 \\
   \Rightarrow O{D^2} = 18 \\
   \Rightarrow OD = \sqrt {18} = 3\sqrt 2 \\
 $

Thus the length of OD is $3\sqrt 2 $ cm.

Note: Although we have proved the above result for rectangles, this will hold true for squares also. Since we have only used the property of square that it’s opposite sides are parallel and equal and all of its angles are ${90^ \circ }$ and this property is also followed by square, thus the result will be equally valid for squares.