Question

If \[f:R \to R\], then \[f\left( x \right) = x\left| x \right|\] will be
A. many-one-onto
B. one-one-onto
C. many-one-into
D. one-one-into

Answer 1

Hint: Here \[R\] means a set of real numbers. The function \[f:R \to R\] implies that the domain of the given function is \[R\]and corresponding range is also \[R\]. In simple words, if you put real numbers in the function you will get a set of real numbers. Plot the graph for the given function. So, use this concept to reach the solution of the problem.

Complete step-by-step answer:
Given, \[f:R \to R\], \[f\left( x \right) = x\left| x \right|\]
This function can be redefined as
\[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
  { - {x^2},}&{x < 0} \\
  {0,}&{x = 0} \\
  {{x^2}}&{x > 0}
\end{array}} \right\}\]
If we plot the graph for \[f\left( x \right)\], it will be

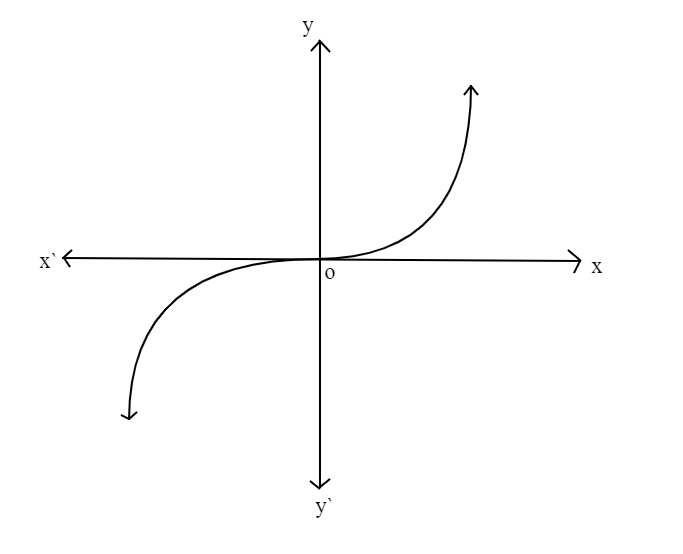
Here the function \[f:R \to R\] is bijective since its graph meets every horizontal and vertical line exactly once.
Since, the graph of \[f\left( x \right)\] shows that it is a bijective (one-one-onto) function.
Thus, the correct option is D. one-one-into.

Note: Here a one-one function is a function of which the answers never repeat. If each element in the codomain ‘Y’ has at least one pre-image in the domain ‘X’ then the function is said to be onto. For a bijective function both one-one and onto functions must be satisfied.