Question

If each side of the rectangle is increased by 20%, then the percentage increase in its area is:
(a) 40%
(b) 20%
(c) 44%
(d) 30%

Answer 1

Hint: We start solving the problem by assigning the variables for the length, breadth and area of the rectangle. We then find this area of the rectangle by using the fact that the area of the rectangle is defined as the product of its length and breadth. We then find the new length and breadth of the rectangle by using the fact that a% of b as $\dfrac{a}{100}\times b$. We then find the new area of the rectangle by multiplying the new length and new breadth of the rectangle. We then find the percentage change in area by using $\dfrac{\text{new area }-\text{ old area}}{\text{old area}}\times 100$.

Complete step by step answer:
According to the problem, we need to find the percentage increase in area of the rectangle if each side of the rectangle is increased by 20%.
Let us assume the original length, breadth and area of the rectangle be ‘l’, ‘b’ and ‘A’.

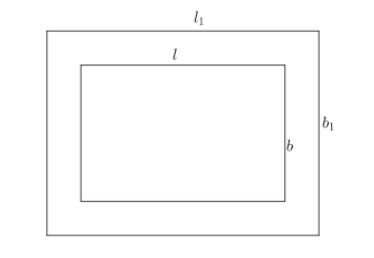
We know that the area of the rectangle is defined as the product of its length and breadth.
So, we have $A=l\times b$ ----(1).
Now, the length and breadth of the rectangle are increased by 20%.
So, the new length of the rectangle is $\left( 100+20 \right)%=120%$ of the original length of the rectangle.
So, the new length $\left( {{l}_{1}} \right)$ = 120% of the original length of the rectangle.
We know that a% of b is defined as $\dfrac{a}{100}\times b$.
So, we have ${{l}_{1}}=\dfrac{120}{100}\times l$.
$\Rightarrow {{l}_{1}}=1.2l$ ---(2).
Similarly, we get the new breadth as ${{b}_{1}}=1.2b$ ---(3).
Let us find the new area $\left( {{A}_{1}} \right)$ of the rectangle.
$\Rightarrow {{A}_{1}}={{l}_{1}}\times {{b}_{1}}=1.2l\times 1.2b$.
$\Rightarrow {{A}_{1}}=1.44lb$.
From equation (1), we get ${{A}_{1}}=1.44A$ ---(4).
Now, let us find the percentage increase in area of the rectangle.
We know that percentage increase in area is defined as $\dfrac{\text{new area }-\text{ old area}}{\text{old area}}\times 100$.
So, we have a percentage increase in area = $\dfrac{1.44A-A}{A}\times 100$.
$\Rightarrow $ Percentage increase in area = $\dfrac{0.44A}{A}\times 100$.
$\Rightarrow $ Percentage increase in area = $0.44\times 100$.
$\Rightarrow $ Percentage increase in area = $44%$.
So, we have found the percentage increase in area as 44%.

So, the correct answer is “Option c”.

Note: Whenever we get this type of problems, we should first assign variables to the unknowns present in the problem. We need to perform each step carefully in order to avoid mistakes while solving the problem. We should not just multiply 20% with 20% and say 400%, which is the most common mistake made by students. Similarly, we can expect problems to find the increase in perimeter of the rectangle.