Question

If $\Delta DEF \sim \Delta MNK. $ If$DE = 2,{\text{ }}MN = 5$, then find the value of$\dfrac{{A\left( {\Delta DEF} \right)}}{{A\left( {\Delta MNK} \right)}}$ by using the property of similar triangles.

Answer 1

Hint: If two triangles are similar then the ratio of their respective sides are same i.e. (SSS congruence).
$ \Rightarrow \dfrac{{DE}}{{MN}} = \dfrac{{EF}}{{NK}} = \dfrac{{FD}}{{KM}}$

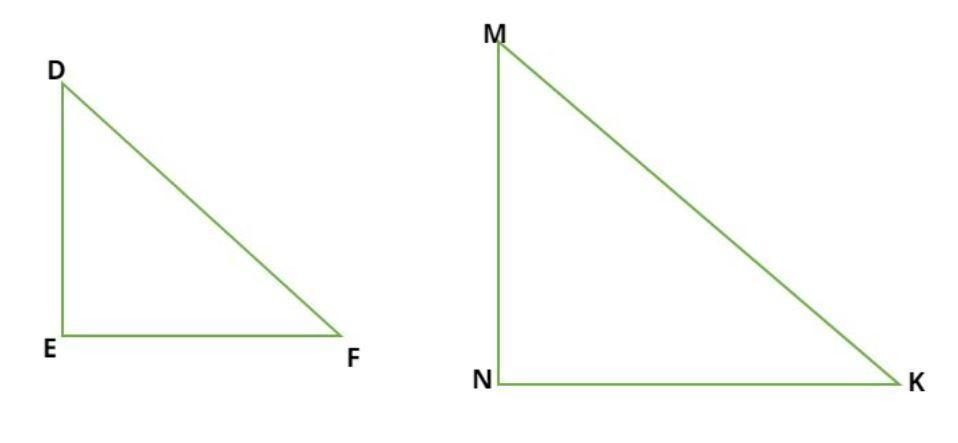
Consider the similar triangles DEF and MNK as shown in figure.
By the property of similar triangles, if two triangles are similar then the ratio of their respective sides are same i.e. (SSS congruence).
$ \Rightarrow \dfrac{{DE}}{{MN}} = \dfrac{{EF}}{{NK}} = \dfrac{{FD}}{{KM}}$
Now it is given that $DE = 2,{\text{ }}MN = 5$
$ \Rightarrow \dfrac{{DE}}{{MN}} = \dfrac{{EF}}{{NK}} = \dfrac{{FD}}{{KM}} = \dfrac{2}{5}...............\left( a \right)$
Now, we consider both as right angle triangle
So, the area of the right angle triangle is half multiplied by base time’s perpendicular.
$
   \Rightarrow A\left( {\Delta DEF} \right) = \dfrac{1}{2}\left( {EF} \right)\left( {DE} \right).............\left( 1 \right) \\
   \Rightarrow A\left( {\Delta MNK} \right) = \dfrac{1}{2}\left( {NK} \right)\left( {MN} \right).............\left( 2 \right) \\
$
So, divide equation (1) from equation (2)
$ \Rightarrow \dfrac{{A\left( {\Delta DEF} \right)}}{{A\left( {\Delta MNK} \right)}} = \dfrac{{\dfrac{1}{2}\left( {EF} \right)\left( {DE} \right)}}{{\dfrac{1}{2}\left( {NK} \right)\left( {MN} \right)}} = \dfrac{{\left( {EF} \right)\left( {DE} \right)}}{{\left( {NK} \right)\left( {MN} \right)}}..........\left( 3 \right)$
Now from equation (a)
$\dfrac{{DE}}{{MN}} = \dfrac{{EF}}{{NK}} = \dfrac{2}{5}$
Therefore from equation (3)
$ \Rightarrow \dfrac{{A\left( {\Delta DEF} \right)}}{{A\left( {\Delta MNK} \right)}} = \dfrac{{\left( {EF} \right)\left( {DE} \right)}}{{\left( {NK} \right)\left( {MN} \right)}} = {\left( {\dfrac{{DE}}{{MN}}} \right)^2}$
$ \Rightarrow \dfrac{{A\left( {\Delta DEF} \right)}}{{A\left( {\Delta MNK} \right)}} = {\left( {\dfrac{{DE}}{{MN}}} \right)^2} = {\left( {\dfrac{2}{5}} \right)^2} = \dfrac{4}{{25}}$
So, this is the required ratio of the area of triangle DEF to triangle MNK.

Note: In such types of questions always remember the key concept which is if two triangles are similar then the ratio of their respective sides are same i.e. (SSS congruence), and always remember the area of the right angle triangle which is stated above then using these properties calculate the ratio of the area of triangle DEF to triangle MNK which is the required answer.