Question

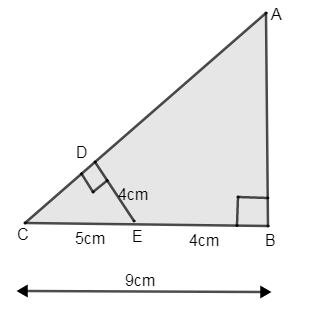
If DE = 4cm, CE = 5cm and BC = 9cm. Find CD, AB and AC from the given figure.

Answer 1

Hint: First consider \[\vartriangle CDE\], find the length of the CD using the Pythagoras theorem. By using the similarity of both the triangles, the ratio of length of their sides will be proportional. Find length of AB. Then by using Pythagoras theorem in \[\vartriangle ABC\], find the length of AC.

Complete step-by-step answer:
Given to us a right angled triangle ABC and values of the sides of \[\vartriangle ABC\].
i.e. DE = 4cm, CE = 5cm and BC = 9cm.
Here, the length of BC = 9cm.
BC = CE + EB
We know the length of BC and CE.
Let’s find the length of EB.

\[\begin{align}
 & 9=5+EB \\
 &\Rightarrow EB=9-5=4cm \\
\end{align}\]
Now let us consider \[\vartriangle ABC\]and the smaller right angled triangle DEC.
The 2 triangles are similar i.e. the ratio of the length of sides of both triangles are proportional.
Here AB and ED are both altitudes in \[\vartriangle ABC\]and \[\vartriangle CDE\] and BC and DC are both bases of the triangle ABC and CDR.
Therefore as the triangles are similar, we can write that,
\[\dfrac{AB}{ED}=\dfrac{BC}{DC}-(1)\]
Now let us go back to \[\vartriangle CDE\], by using the Pythagoras theorem, we know that,
\[\begin{align}
 & C{{E}^{2}}=C{{D}^{2}}+D{{E}^{2}} \\
 & \Rightarrow C{{D}^{2}}=C{{E}^{2}}-D{{E}^{2}} \\
 & CD=\sqrt{C{{E}^{2}}-D{{E}^{2}}} \\
\end{align}\]
From the figure we know that CE = 5cm and DE = 4cm.
\[\therefore \] Length of \[CD=\sqrt{{{5}^{2}}-{{4}^{2}}}=\sqrt{25-16}=\sqrt{9}=3cm\].
\[\therefore \] Length of CD = 3cm.
Now, let us consider equation (1), we know the lengths of ED, BC and DC.
Substitute and find the length of AB.
\[\begin{align}
 & \dfrac{AB}{ED}=\dfrac{BC}{DC} \\
 & \Rightarrow \dfrac{AB}{4}=\dfrac{9}{3} \\
 & \therefore AB=\dfrac{4\times 9}{3}=4\times 3=12cm \\
\end{align}\]
\[\therefore \] Length of AB = 12cm.
Now we need to find the length of AC.
Consider \[\vartriangle ABC\], by Pythagoras theorem,
\[\begin{align}
 & A{{C}^{2}}=A{{B}^{2}}+C{{D}^{2}} \\
 & AC=\sqrt{A{{B}^{2}}+C{{D}^{2}}} \\
\end{align}\]
We know AB = 12cm and CD = 9cm. Substitute and find the value of AC.
\[\therefore AC=\sqrt{{{12}^{2}}+{{9}^{2}}}=\sqrt{144+81}=\sqrt{225}=15cm\]
\[\therefore \] Length of AC = 15cm.
Hence, we got all the required lengths as,
CD = 3cm, AB = 12cm and AC = 15cm.

Note: In our two right angles triangles, the corresponding sides are in the same ratio. Hence the matching angles are also the same. Thus we have considered the ratio of their sides \[\dfrac{AB}{ED}\] and \[\dfrac{BC}{DC}\], which are equal. The two triangles can be also proved by SSS congruence i.e. all the sides of the two triangles are similar.