If d is the HCF of 45 and 27 , then x,y satisfying d=27x+45y are:
A) $x=2,y=1$
B) $x=2,y=-1$
C) $x=-1,y=2$
D) $x=-1,y=-2$
Answer
Verified359.1k+ views
Hint: The given question is related to the highest common factor of two numbers and linear equations in two variables. Find the highest common factor of \[45\] and \[27\], then draw the line represented by the equation $d=27x+45y$ on a graph and check the points that lie on the line.
Complete step-by-step answer:
To solve the question, first we have to find the highest common factor of \[45\] and \[27\]. We will use the factorization method to find the value of the highest common factor of \[45\] and \[27\]. In factorization method, we write the numbers as a product of prime numbers and then find the highest number that is common in both.
\[45\] can be written as $45=3\times 3\times 5$ and \[27\] can be written as $27=3\times 3\times 3$. We can see that the highest number common in both is $3\times 3=9$. So, the highest common factor of \[45\] and \[27\] is $9$. We are given that the highest common factor of \[45\] and \[27\] is $d$ . So, $d=9$.
Now, we are given the equation $d=27x+45y$. Substituting $d=9$ in the equation, we get $9=27x+45y$. On rearranging the equation to make it of the form $y=mx+c$, we get $y=\dfrac{-27}{45}x+\dfrac{1}{5}$. So, the equation represents a line with slope $m=\dfrac{-27}{45}$ and $y$ intercept $c=\dfrac{1}{5}$.
The line is shown on the graph as:
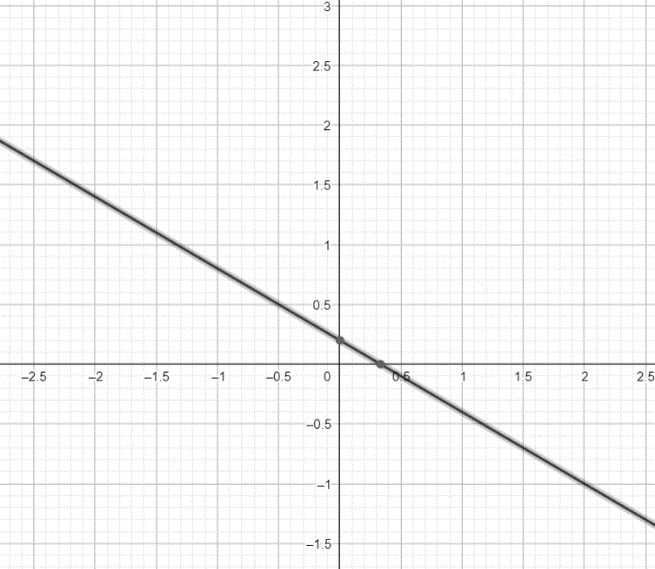
Now, we will plot the points corresponding to the given options on the line. The points lying on the line will satisfy the equation $d=27x+45y$. The points corresponding to the options are:
Option A. $(2,1)$ ; Option B. $(2,-1)$ ; Option C. $(-1,2)$; Option D. $(-1,-2)$.
The points are plotted on the graphs as:
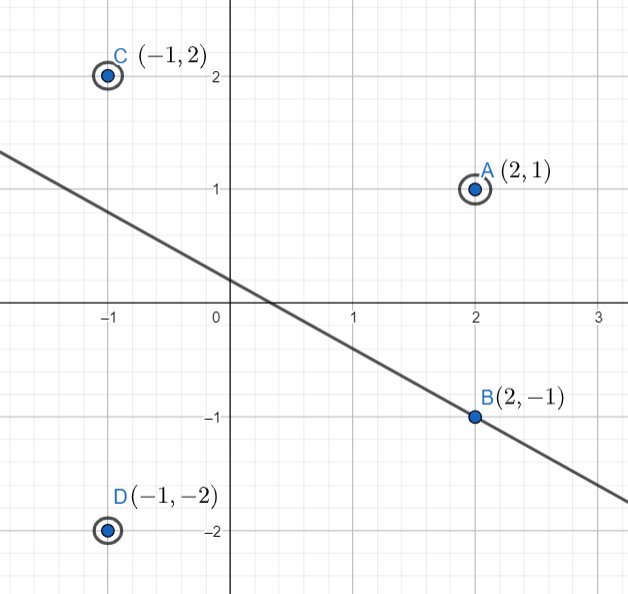
From the graph we can see that $B(2,-1)$ is the only point lying on the line. So, the values of $x$ and $y$ satisfying $d=27x+45y$ are $x=2,y=-1$, where $d$ is the highest common factor of \[45\] and \[27\].
Hence, option B. is the correct answer.
Note: The correct answer can also be found by substituting the values of $x$ and $y$ from each option in the equation. But it will be time taking. So, it is better to plot the line and points on the graph to find the values of $x$ and $y$ satisfying the equation.
Complete step-by-step answer:
To solve the question, first we have to find the highest common factor of \[45\] and \[27\]. We will use the factorization method to find the value of the highest common factor of \[45\] and \[27\]. In factorization method, we write the numbers as a product of prime numbers and then find the highest number that is common in both.
\[45\] can be written as $45=3\times 3\times 5$ and \[27\] can be written as $27=3\times 3\times 3$. We can see that the highest number common in both is $3\times 3=9$. So, the highest common factor of \[45\] and \[27\] is $9$. We are given that the highest common factor of \[45\] and \[27\] is $d$ . So, $d=9$.
Now, we are given the equation $d=27x+45y$. Substituting $d=9$ in the equation, we get $9=27x+45y$. On rearranging the equation to make it of the form $y=mx+c$, we get $y=\dfrac{-27}{45}x+\dfrac{1}{5}$. So, the equation represents a line with slope $m=\dfrac{-27}{45}$ and $y$ intercept $c=\dfrac{1}{5}$.
The line is shown on the graph as:
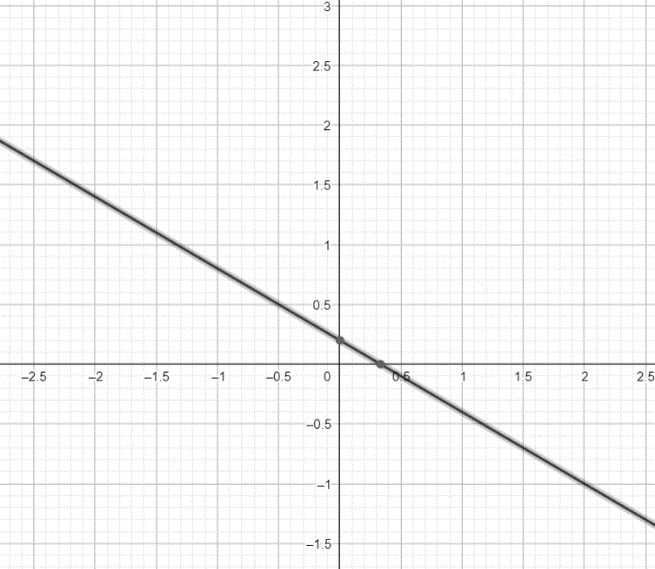
Now, we will plot the points corresponding to the given options on the line. The points lying on the line will satisfy the equation $d=27x+45y$. The points corresponding to the options are:
Option A. $(2,1)$ ; Option B. $(2,-1)$ ; Option C. $(-1,2)$; Option D. $(-1,-2)$.
The points are plotted on the graphs as:
From the graph we can see that $B(2,-1)$ is the only point lying on the line. So, the values of $x$ and $y$ satisfying $d=27x+45y$ are $x=2,y=-1$, where $d$ is the highest common factor of \[45\] and \[27\].
Hence, option B. is the correct answer.
Note: The correct answer can also be found by substituting the values of $x$ and $y$ from each option in the equation. But it will be time taking. So, it is better to plot the line and points on the graph to find the values of $x$ and $y$ satisfying the equation.
Last updated date: 17th Sep 2023
•
Total views: 359.1k
•
Views today: 3.59k
