Question

If $ \cos \theta =\dfrac{5}{13} $ , find the value of $ \dfrac{2\sin \theta -{{\cos }^{2}}\theta }{2\sin \theta \cos \theta }\times \dfrac{1}{{{\tan }^{2}}\theta } $ . \[\]

Answer 1

Hint:
We recall the definitions of sine, cosine and tangent trigonometric ratios from the right angled triangle. We take the length of the adjacent side as $ b=5 $ and hypotenuse as $ h=13 $ . We find the side $ b $ using Pythagoras theorem. We find $ \sin \theta =\dfrac{p}{h},\tan \theta =\dfrac{p}{b} $ and put the values in given trigonometric expression.\[\]

Complete step by step answer:
We know that in right angled triangle (here $ \Delta ABC $ ) the side opposite to right angled triangle is called hypotenuse denoted as $ h=AC $ , the vertical side is called perpendicular denoted as $ p=AB $ and the horizontal side is called the base denoted as $ b=BC $ .\[\]

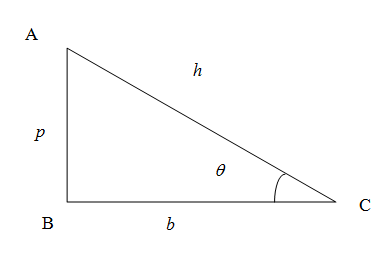
We know from the trigonometric ratios in a right angled triangle the sine of any angle is given by the ratio of side opposite to the angle to the hypotenuse. In the figure the sine of the angle $ \theta $ is given by
\[\sin \theta =\dfrac{p}{h}\]
Similarly the cosine of an angle is the ratio of side adjacent to the angle (excluding hypotenuse) to the hypotenuse. So we have cosine of angle $ \theta $
\[\cos \theta =\dfrac{b}{h}.\]
The tangent of the angle is the ratio of opposite side to the adjacent side (excluding hypotenuse) . So we have tangent of the angle of angle $ \theta $
\[\tan \theta =\dfrac{p}{b}\]
 We know from Pythagoras theorem that “in a right-angled triangle the square of the hypotenuse is the sum of squares of the other two sides”. So in triangle we have
\[\begin{align}
  & {{h}^{2}}={{p}^{2}}+{{b}^{2}} \\
 & \Rightarrow {{p}^{2}}={{h}^{2}}-{{b}^{2}} \\
 & \Rightarrow p=\sqrt{{{h}^{2}}-{{b}^{2}}} \\
\end{align}\]
We are give in the question that $ \cos \theta =\dfrac{5}{13} $ . So we have;
\[\cos \theta =\dfrac{5}{13}=\dfrac{b}{h}\]
So let us take $ b=5,h=13 $ . So we have
\[p=\sqrt{{{13}^{2}}-{{5}^{2}}}=\sqrt{169-25}=\sqrt{144}=12\]
So we have sine and tangent of the angle as;
  $ \begin{align}
  & \sin \theta =\dfrac{p}{h}=\dfrac{12}{13} \\
 & \tan \theta =\dfrac{p}{b}=\dfrac{12}{5} \\
\end{align} $
We pout the obtained values of \[\sin \theta =\dfrac{12}{13},\tan \theta =\dfrac{12}{5}\] and give value of $ \cos \theta =\dfrac{5}{13} $ in the given expression to have;
\[\begin{align}
  & \dfrac{2\sin \theta -{{\cos }^{2}}\theta }{2\sin \theta \cos \theta }\times \dfrac{1}{{{\tan }^{2}}\theta } \\
 & \Rightarrow \dfrac{2\times \dfrac{12}{13}-\dfrac{{{5}^{2}}}{{{13}^{2}}}}{2\times \dfrac{12}{13}\times \dfrac{5}{13}}\times \dfrac{1}{{{\left( \dfrac{12}{5} \right)}^{2}}} \\
 & \Rightarrow \dfrac{\dfrac{2\times 12\times 13-{{5}^{2}}}{{{13}^{2}}}}{\dfrac{2\times 12\times 5}{{{13}^{2}}}}\times \dfrac{{{5}^{2}}}{{{12}^{2}}} \\
\end{align}\]
We cancel out $ {{13}^{2}} $ from the numerator and denominator to have;
\[\begin{align}
  & \Rightarrow \dfrac{312-25}{120}\times \dfrac{25}{144} \\
 & \Rightarrow \dfrac{287}{24}\times \dfrac{5}{144}=\dfrac{1435}{3456} \\
\end{align}\]
So the evaluated value is $ \dfrac{1435}{3456} $ .\[\]
Note:
 We can alternatively solve by using Pythagorean trigonometric identity $ {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 $ to find $ \sin \theta $ and the $ \tan \theta $ from $ \tan \theta =\dfrac{\sin \theta }{\cos \theta } $ . We note that lengths are always positive and that we have taken positive square roots only. The reciprocal ratios of sine, cosine and tangent are given as $ \operatorname{cosec}\theta =\dfrac{h}{p},\sec \theta =\dfrac{h}{b},\cot \theta =\dfrac{b}{p} $ .