Question

If \[APB\] and $ CQD $ are two parallel lines, then bisectors of $ \angle APQ $ , $ \angle BPQ,\angle CQP $ and $ \angle PQD $ forms
A. a square
B. a rhombus
C. a rectangle
D. any other parallelogram

Answer 1

Hint: First we draw two parallel lines \[APB\] and $ CQD $ , then, we draw angle bisectors of $ \angle APQ $ , $ \angle BPQ,\angle CQP $ and $ \angle PQD $ . Assuming that these angle bisectors meet at point $ M $ and $ N $ . By joining points we draw a quadrilateral, then by observing the property of quadrilateral forms, we choose the correct answer.

Complete step-by-step answer:
Let us first draw a diagram by using information given that \[APB\] and $ CQD $ are two parallel lines and there are angle bisectors of $ \angle APQ $ , $ \angle BPQ,\angle CQP $ and $ \angle PQD $ .

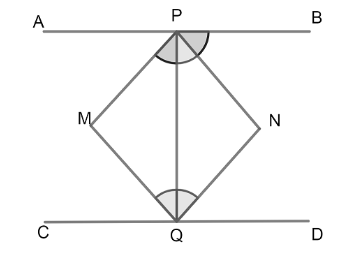
We have given that \[APB\] and $ CQD $ are two parallel lines. Let us assume that the bisectors of $ \angle APQ $ and $ \angle CQP $ meet at point $ M $ . Similarly, bisectors of $ \angle BPQ $ and $ \angle DQP $ meet at point $ N $ .
We join $ PM,QM,QN,PN $ , it forms a quadrilateral.
Now, as given $ APB\parallel CQD $
So, alternate interiors angles will be equal $ \angle APQ=\angle PQD $
Now, as $ PM $ and $ QN $ are angle bisectors of $ \angle APQ $ and $ \angle PQD $ respectively. So,
 $ \angle APM=\angle MPQ $ and $ \angle BPN=\angle NPQ $
 $ \angle MPQ=\angle NQP $
As these are alternate interior angles so the lines $ PM $ and $ QN $ must be parallel.
Similarly, alternate interiors angles $ \angle BPQ=\angle CQP $ are also equal.
So, the lines $ PN $ and $ QM $ must be parallel.
As $ PM\parallel QN $ and $ PN\parallel QM $ .
Opposite sides are parallel to each other, it means $ PMQN $ is a parallelogram.
As $ CQD $ is a straight line, so the measure of $ \angle CQD=180{}^\circ $
Or we can write as $ \angle CQP+\angle DQP=180{}^\circ $
Or $ \angle CQM+\angle PQM+\angle DQN+\angle PQN=180{}^\circ $
As $ PM $ and $ QN $ are angle bisectors, So, $ \angle PQM+\angle PQM+\angle PQN+\angle PQN=180{}^\circ $
\[\left[ \angle CQM=\angle PQM\And \angle DQN=\angle PQN \right]\]
\[\begin{align}
  & 2\angle PQM+2\angle PQN=180{}^\circ \\
 & 2\left( \angle PQM+\angle PQN \right)=180{}^\circ \\
 & \angle PQM+\angle PQN=\dfrac{180{}^\circ }{2} \\
 & \angle PQM+\angle PQN=90{}^\circ \\
\end{align}\]
\[\angle MQN=90{}^\circ \]
So, the correct answer is “Option C”.

Note: Opposite sides of a rectangle are always equal and parallel to each other. Diagonals of a rectangle bisect each other. Measure of angles of a rectangle is equal to \[90{}^\circ \]. It is important to apply properties to prove it a quadrilateral. Also, applying properties is important as given in the options all are quadrilateral so we have to prove that it is a rectangle.