-
Courses-
Crash Courses 2021
-
Olympiads/NTSE/Others
-
Micro Courses
-
Vedantu Super Kids NEW
-
Reading & Spoken English -
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
Questions & Answers
Question
Answers
Related Questions
If $ABCDEF$ is a regular hexagon. Find each interior angle of $\vartriangle ABE$ .
Answer
![Verified]()
Verified
Verified
Hint- To find out the angles of $\vartriangle ABE$, first determine each angle of hexagon by the help of general formula of net angle for regular polygon. Then find each equal angle and further proceed with the help of diagram.
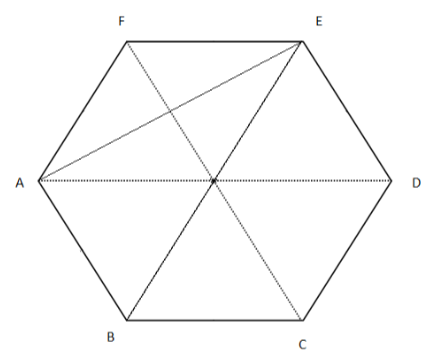
Given that $ABCDEF$ is a regular hexagon,
So all the sides will be equal in length.
Also we know that for $n - $ sided polygon.
Sum of all the interior angles $ = (n - 2) \times {180^0}$.
Hence, sum of all the interior angles of hexagon is
$
= (6 - 2) \times {180^0} \\
= 4 \times {180^0} \\
= {720^0} \\
$
Also we know that for regular hexagon, all the interior angles are same so each angle
$
= \dfrac{{{{720}^0}}}{6} \\
= {120^0}...........(1) \\
$
Quadrilateral $ABEF$ is a $4$ sided polygon.
Sum of its interior angle
\[
= \left( {4 - 2} \right){180^0} \\
= 2 \times {180^0} \\
= {360^0} \\
\]
As \[\angle AFE = {120^0}........(2)\] [from equation (1)]
In $\vartriangle AFE,$
$AF = EF.........(3)$ [Since they are sides of regular polygon]
$ \Rightarrow \angle FAE = \angle FEA$ [Since angles opposite to equal sides are equal]
$\angle FAE + \angle FEA + \angle AFE = {180^0}$ [Sum of all the angle of triangle is \[{180^0}\] ]
From equation (2) and equation (3) substituting the value
$
\Rightarrow \angle FAE + \angle FEA + {120^0} = {180^0} \\
\Rightarrow \angle FAE + \angle FEA = {60^0} \\
\Rightarrow \angle FAE = \angle FEA = {30^0}[\because \angle FAE = \angle FEA] \\
$
Since,\[\angle FAE + \angle EAB = {120^0}\] [Angle of a regular hexagon]
$
\therefore \angle EAB = {90^0}..........(4) \\
\angle ABE = \dfrac{1}{2} \times {120^0}\left[ {\because \angle ABE{\text{ bisects }}\angle ABC} \right]
\\
= {60^0} \\
$
Now moving on to triangle $ABE$
In $\vartriangle ABE$
$\angle AEB + \angle ABE + \angle EBA = {180^0}$ [Sum of all the angles of a triangle]
$\angle AEB = {180^0} - {60^0} - {90^0} = {30^0}$ [From equation (4) and equation (5)]
Hence all the angles of $\vartriangle ABE$ are
$\angle ABE = {60^0},\angle EAB = {90^0}\& \angle AEB = {30^0}$
Note- In order to solve such kind of questions of geometry, figure is a must in order to have a better understanding of the angles. Also all the general properties of triangles and polygons, like the sum of interior angles and relationship between the sides and angles, must be remembered. As, these properties are very handy in solving such problems.
Given that $ABCDEF$ is a regular hexagon,
So all the sides will be equal in length.
Also we know that for $n - $ sided polygon.
Sum of all the interior angles $ = (n - 2) \times {180^0}$.
Hence, sum of all the interior angles of hexagon is
$
= (6 - 2) \times {180^0} \\
= 4 \times {180^0} \\
= {720^0} \\
$
Also we know that for regular hexagon, all the interior angles are same so each angle
$
= \dfrac{{{{720}^0}}}{6} \\
= {120^0}...........(1) \\
$
Quadrilateral $ABEF$ is a $4$ sided polygon.
Sum of its interior angle
\[
= \left( {4 - 2} \right){180^0} \\
= 2 \times {180^0} \\
= {360^0} \\
\]
As \[\angle AFE = {120^0}........(2)\] [from equation (1)]
In $\vartriangle AFE,$
$AF = EF.........(3)$ [Since they are sides of regular polygon]
$ \Rightarrow \angle FAE = \angle FEA$ [Since angles opposite to equal sides are equal]
$\angle FAE + \angle FEA + \angle AFE = {180^0}$ [Sum of all the angle of triangle is \[{180^0}\] ]
From equation (2) and equation (3) substituting the value
$
\Rightarrow \angle FAE + \angle FEA + {120^0} = {180^0} \\
\Rightarrow \angle FAE + \angle FEA = {60^0} \\
\Rightarrow \angle FAE = \angle FEA = {30^0}[\because \angle FAE = \angle FEA] \\
$
Since,\[\angle FAE + \angle EAB = {120^0}\] [Angle of a regular hexagon]
$
\therefore \angle EAB = {90^0}..........(4) \\
\angle ABE = \dfrac{1}{2} \times {120^0}\left[ {\because \angle ABE{\text{ bisects }}\angle ABC} \right]
\\
= {60^0} \\
$
Now moving on to triangle $ABE$
In $\vartriangle ABE$
$\angle AEB + \angle ABE + \angle EBA = {180^0}$ [Sum of all the angles of a triangle]
$\angle AEB = {180^0} - {60^0} - {90^0} = {30^0}$ [From equation (4) and equation (5)]
Hence all the angles of $\vartriangle ABE$ are
$\angle ABE = {60^0},\angle EAB = {90^0}\& \angle AEB = {30^0}$
Note- In order to solve such kind of questions of geometry, figure is a must in order to have a better understanding of the angles. Also all the general properties of triangles and polygons, like the sum of interior angles and relationship between the sides and angles, must be remembered. As, these properties are very handy in solving such problems.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
