Question

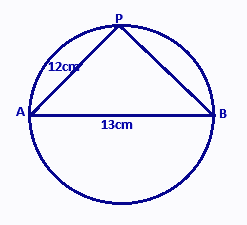
If AB is the diameter of the circle and AB=13cm, AP=12cm. then find PB=?

Answer 1

Hint: From the figure AB is the diameter and the angle so inscribed in the semicircle by that diameter is a right angle. So \[\angle APB = {90^ \circ }\]. Thus we can use Pythagoras theorem to find the side PB by taking diameter as the hypotenuse. Let’s solve it.

Step by step solution:
Given that AB is a diameter of the circle and the angle formed by the diameter is a right angle.

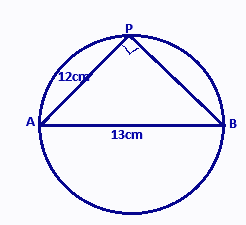
So using the Pythagoras theorem,
\[A{B^2} = A{P^2} + P{B^2}\]
To find PB,
\[ \Rightarrow P{B^2} = A{B^2} - A{P^2}\]
Putting the values,
\[ \Rightarrow P{B^2} = {13^2} - {12^2}\]
\[ \Rightarrow P{B^2} = 169 - 144\]
\[ \Rightarrow P{B^2} = 25\]
Taking the square root on both sides,
\[ \Rightarrow PB = 5cm\]

This is the length of side PB of the triangle so formed \[ \Rightarrow PB = 5cm\]

Note:
Students don’t consider that AP and PB are both chords so they will measure the same length. Also it is not given that both the base angles are of \[{45^ \circ }\]. So we have enlisted the property that the angle formed by the diameter is a right angle. So go with it only.