Question

If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.

Answer 1

Hint: - Area of circle is $\pi {r^2}{\text{ sq}}{\text{.units}}$, where r is the radius of the circle.

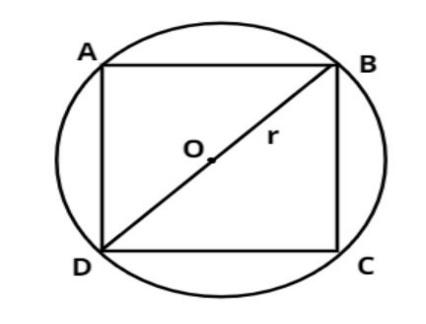
Let, we assume ABCD is a square inscribed in a circle with center O.
Let the side of the square be $b$.
$ \Rightarrow AB = BC = CD = DA = b$.
Let the radius of the circle be $r$.
$ \Rightarrow OB = OD = r$
As we know area of the circle$ = \pi {r^2}{\text{ sq}}{\text{.units}}$
And the diagonal of the square $\left( {DB} \right)$is passing through the center O.
Which is the diameter of the circle.
$ \Rightarrow BD = 2r$
And we know that the side of a square is perpendicular to each other.
Therefore from figure $\Delta BCD{\text{ }}$makes a right angle triangle so, apply Pythagoras Theorem
$\begin{gathered}
   \Rightarrow {\left( {BD} \right)^2} = {\left( {BC} \right)^2} + {\left( {CD} \right)^2} \\
   \Rightarrow {\left( {2r} \right)^2} = {b^2} + {b^2} = 2{b^2} \\
   \Rightarrow {b^2} = \dfrac{{4{r^2}}}{2} \Rightarrow 2{r^2} \\
\end{gathered} $
As we know area of square is $ = {\left( {{\text{side}}} \right)^2} = {b^2} = 2{r^2}{\text{ sq}}{\text{.units}}$
Now we have to find out the ratio of the areas of the circle and the square.
Therefore required ratio $ = \dfrac{{{\text{Area of circle}}}}{{{\text{Area of square}}}} = \dfrac{{\pi {r^2}{\text{ sq}}{\text{.units}}}}{{{\text{2}}{{\text{r}}^2}{\text{ sq}}{\text{.units}}}} = \dfrac{\pi }{2}$
So, $\dfrac{\pi }{2}$ is the required ratio of the areas.
Note: -In such types of questions the key concept we have to remember is that the diagonal of the square is always passing through the center of the circle, and the sides of square is perpendicular to each other so triangle BCD makes a right angle triangle from this we easily calculate the side of the square, then find out the area of the circle and area of the square, then divide them we will get the required answer.