Question

If a point C lies between two points A and B such that AC=BC, then prove that $AC=\dfrac{1}{2}AB$. Explain by drawing the figure.

Answer 1

Hint: Draw the figure. As AC=BC, So use the fourth axiom and substitute AC=BC and simplify it.
You will get the answer.

So it is mentioned in the question that a point C lies between two points $A$ and $B$ such that $AC=BC$.
So we can say that point $C$ is the midpoint of $AB$.
And we have to prove that $AC=\dfrac{1}{2}AB$.
So we have to use Euclid's postulates.
A straight line segment can be drawn joining any two points.

Any straight line segment can be extended indefinitely in a straight line.

Given any straight lines segment, a circle can be drawn having the segment as radius and one endpoint as center.

All Right Angles are congruent.

5. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two Right Angles, then the two lines inevitably must intersect each other on that side if extended far enough. This postulate is equivalent to what is known as the Parallel Postulate.

Now using Euclid's first postulate,
Which is stated as “A straight line segment can be drawn joining any two points”.
So let us take a line joining two points $A$ and $B$.

So now point $C$ lies between $A$ and $B$ such that $AC=BC$.
So $C$ is the midpoint of $AB$.

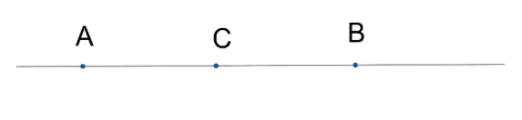
So by the fourth axiom,
If two quantities coincide with each other then they are equal to each other.
So the two quantities are $AC$ and $BC$ they both coincide on $AB$.
So we get,
$AC+BC=AB$
So we have given in the question that $AC=BC$.
So substituting $AC=BC$ in above we get,
$AC+AC=AB$
So now simplifying above in a simple manner we get,
$2AC=AB$
Now dividing above by $2$,
So by simplifying we get,
$AC=\dfrac{AB}{2}$
So we have got the proof which is $AC=\dfrac{AB}{2}$.
Hence proved.

Note: Read the question in a careful manner. You should be familiar with Euclid's postulates. Also, don’t jumble yourself with which postulates to apply. Solve it in a simple manner. Don’t confuse yourself between axiom and postulate.