Question

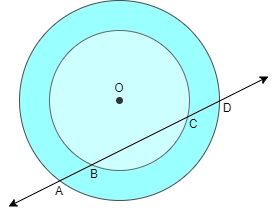
If a line intersects two concentric circles (circle with same center) with center O at A, B, C and D, prove that AB = CD (see figure)

Answer 1

Hint: To show that side AB = CD prove that$\Delta OAB \simeq \Delta {\text{OCD}}$ using the property of triangle Side-Angle-Side and also remember to join A, B, C and D to the center of the circles O to form the triangles, use this information to approach the solution.

Complete step-by-step answer:
Before attempting this question let’s join A to O, B to O, C to O and D to O so the figure will be

Since we know that OA and OD are the radius of the outer circle and OB and OC are the radius of the inner circle
Therefore, OA = OD
And OB = OC
In $\Delta OBC$ we know that
OB = OC
So as angles opposite to equal sides are equal
Therefore, $\angle OBC = \angle OCB$
Similarly, in $\Delta OAD$
As $OA = OD$ and angles opposite to equal sides are equal
Therefore, $\angle OAD = \angle ODA$
As $\angle OBA$ and $\angle OBC$ lie on the same straight line
Therefore, $\angle OBA + \angle OBC = {180^ \circ }$ (equation 1)
Similarly, $\angle OCB + \angle OCD = {180^ \circ }$ (equation 2)
Now, solving the equation 1
\[\angle OBA + \angle OBC = {180^ \circ }\]
\[ \Rightarrow \]\[\angle OBA = {180^ \circ } - \angle OBC\]
Since we know that $\angle OBC = \angle OCB$
Therefore, \[\angle OBA = {180^ \circ } - \angle OCB\] (equation 3)
Now solving equation 2
$\angle OCB + \angle OCD = {180^ \circ }$
\[ \Rightarrow \]$\angle OCD = {180^ \circ } - \angle OCB$ (equation 4)
Now comparing the equation 3 and equation 4 we get
$\angle OBA = \angle OCD$
Now in $\Delta OAB$ and $\Delta {\text{OCD}}$
Since we know that OA and OD are the radius of the outer circle and OB and OC are the radius of the inner circle
Therefore, OA = OD
And OB = OC
In the above statement we know that $\angle OBA = \angle OCD$
so, by the property of Side-Angle-Side $\Delta OAB \simeq \Delta {\text{OCD}}$
therefore, by congruence property of SAS postulate AB = CD
Hence proved

Note: Whenever we face such geometry problems the key concept is to prove congruent the two triangles in which the sides that we need to prove equal lies. Taking this approach will eventually help as if the triangles are proved congruent than using congruence property the sides can be proved equal.