Question

If a hexagon $ABCDEF$ circumscribes a circle. Prove that $AB + CD + EF = BC + DE + FA$.

Answer 1

Hint: A tangent, line to a circle is a line that touches the circle at exactly one point, never entering the circle’s interior. The point where the intersection occurs is called the point of tangency. The tangent is always perpendicular to the radius drawn at the point of tangency. Tangents from an external point to a circle are equal.

Complete step-by-step answer:
Let hexagon $ABCDEF$ circumscribes by a circle as shown in figure below:

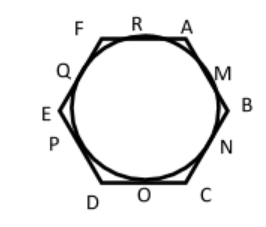
We need to prove that: $AB + CD + EF = BC + DE + FA$.
 As tangents from an external point to a circle are equal.
Therefore,
As $A$ is an external point, therefore $A$
$AM = AR..........(1)$
As $B$ is an external point, therefore
$BM = BN..........(2)$
As $C$ is an external point, therefore
$CN = CO............(3)$
As $D$ is an external point, therefore
$DO = DP...........(4)$
As $E$ is an external point, therefore
$EP = EQ............(5)$ and
As $F$ is an external point, therefore
$FQ = FR............(6)$
By adding (1) and (2), we get
$ \Rightarrow$$AM + BM = AR + BN$
\[ \Rightarrow AB = AR + BN...........(7)\]
By adding (3) and (4), we get
$ \Rightarrow$$CO + DO = CN + DP$
$ \Rightarrow CD = CN + DP...........(8)$
By adding (5) and (6), we get
$ \Rightarrow$$EQ + FQ = EP + FR$
$ \Rightarrow EF = EP + FR.........(9)$
Now by adding (7), (8) and (9) we get,
$ \Rightarrow$$AB + CD + EF = AR + BN + CN + DP + EP + FR$
Now combining $(BN + CN)$, $(DP + EP)$ and $(FR + AR)$ together, we get
$ \Rightarrow$$AB + CD + EF = (BN + CN) + (DP + EF) + (FR + AR)$
As $BN + CN = BC,DP + EP = DE$and$FR + RA = FA$.
$ \Rightarrow AB + CD + EF = BC + DE + FA$.

Note: If a line is tangent to a circle, it is perpendicular to the radius drawn to the point of tangency. Tangent segments to a circle from the same external point are congruent. Also, as we know that a tangent to a circle is perpendicular to the radius through the point of contact. Hence, the tangents drawn from an external point are equal.