Question

If a flag-staff of 6m height placed on top of a tower throws a shadow of $2\sqrt 3 m$ along the ground, then what is the angle that the sun makes with the ground?
$(a){\text{ 6}}{{\text{0}}^0}$
$(b){\text{ 4}}{{\text{5}}^0}$
$(c){\text{ 3}}{{\text{0}}^0}$
$(d){\text{ 1}}{{\text{5}}^0}$

Answer 1

Hint- By the data provided in the question we can easily form a triangle and implementation of trigonometric ratios to this triangle will help to reach the answer.

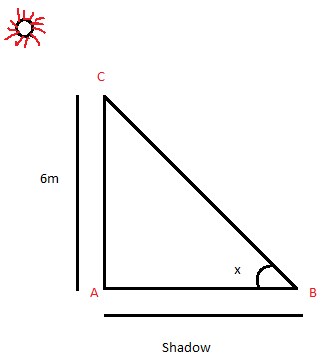
Let us take the angle of elevation made by the point B on the ground with the sun as x degree.
Now length of shadow that is AB =$2\sqrt 3 m$, given in question.
The length of tower AC =6m, given in question.
$\operatorname{Tan} \theta = \dfrac{{height}}{{base}}$……………………………….. (1)
Now in $\vartriangle ABC$
Using equation (1) we can say that
$\operatorname{Tan} x = \dfrac{{AC}}{{AB}} = \dfrac{6}{{2\sqrt 3 }} = \dfrac{3}{{\sqrt 3 }}$
Now let’s rationalize the denominator part by multiplying $\sqrt 3 $ in both the numerator and denominator part.
$\tan x = \dfrac{3}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }} = \dfrac{{3\sqrt 3 }}{3} = \sqrt 3 $
Now
$
  \tan x = \sqrt 3 \\
   \Rightarrow x = {\tan ^{ - 1}}\left( {\sqrt 3 } \right) = \dfrac{\pi }{3} = {60^0} \\
 $
Hence the required angle is 60 degrees.
Note- Whenever we come across this type of question the basic concept that we need to recall is that of trigonometric ratios, example$\operatorname{Tan} \theta = \dfrac{{height}}{{base}}$, similarly all other trigonometric ratios have a default implementation formula. Having a good grasp over them helps to reach the right answer.