Question

How do you graph the line with slope $ - 1/2$ passing through point $( - 3, - 5)$ ?

Answer 1

Hint: First we will start by forming the equation using the information which is the slope of the equation and a point. Here, we are using the slope point form of line which is given by $y = mx + c$. Then finally graph the equation of the line.

Complete step by step solution:
Generally, there are infinitely many such linear equations. Now we know that the slope point form of line is $y = mx + c$ where $m$ is the slope of the line.
$m = - 1/2 \\
\Rightarrow x = - 3 \\
\Rightarrow y = - 5 \\ $
Now, we substitute all these values in the equation $y = mx + c$.
$y = mx + c \\
\Rightarrow - 5 = \left( {\dfrac{{ - 1}}{2}} \right)( - 3) + c \\ $
Now, we will simplify the equation further by cross multiplying the terms.
$- 5 = \left( {\dfrac{{ - 1}}{2}} \right)( - 3) + c \\
\Rightarrow - 10 = 3 + 2c \\ $
Now take all the like terms to one side.
$- 10 = 3 + 2c \\
\Rightarrow - 10 - 3 = 2c \\
 $
Now we will solve for the value of $c$ that is the y-intercept.
$- 10 - 3 = 2c \\
\Rightarrow - 13 = 2c \\
\Rightarrow c = \dfrac{{ - 13}}{2} \\ $
Hence, the value of y-intercept is $\dfrac{{ - 13}}{2}$. Now we will solve for the value of x-intercept by substituting $y = 0$ in the slope point form of line.
\[y = mx + c \\
\Rightarrow 0 = \left( {\dfrac{{ - 1}}{2}} \right)(x) - \dfrac{{13}}{2} \\
\Rightarrow\dfrac{{13}}{2} = \left( {\dfrac{{ - 1}}{2}} \right)x \\
\Rightarrow 13 = - x \\
\therefore x = 13 \\ \]
Hence, the value of x-intercept is $ - 13$. Now we know the y-intercept, x-intercept, slope of the line and the point through which the line passes hence, we will plot the graph.

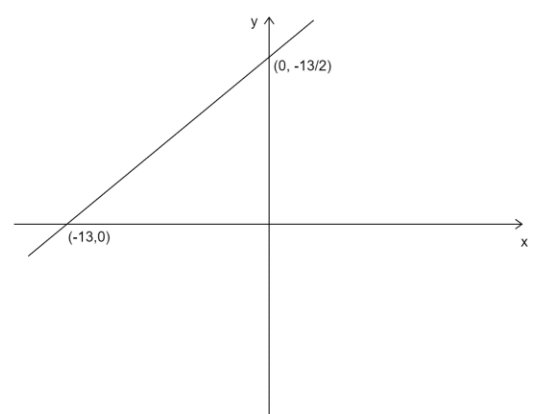
Additional Information:
To cross multiply terms, you will multiply the numerator in the first fraction times the denominator in the second fraction, then you write that number down. Then you multiply the numerator of the second fraction times the number in the denominator of your first fraction, and then you write that number down. By Cross multiplication of fractions, we get to know if two fractions are equal or which one is greater. This is especially useful when you are working with larger fractions that you are not sure how to reduce. Cross multiplication also helps us to solve for unknown variables in fractions.

Note: While cross multiplying the terms, multiply the terms step-by-step to avoid any mistakes. After cross multiplication, take the variables to one side and integer type of terms to the other side. Reduce the terms by factorisation.