
How to graph a parabola $y = {\left( {x + 5} \right)^2} - 3$?
Answer
533.7k+ views
Hint: First, find the x-intercepts of the curve by putting $y = 0$. After that, find the y-intercept by putting $x = 0$. Then take a minimum of 5 points and plot the points. After plotting the points, join the points with a smooth freehand curve and identify the curve that we have obtained.
Complete step by step solution:
We know that the graph of a function is the locus of points $\left( {x,y} \right)$ such that $y = f\left( x \right)$ where x, y are real numbers. We are given the following quadratic polynomial function,
$ \Rightarrow y = {\left( {x + 5} \right)^2} - 3$
So, let us put $y = 0$ and find the x-intercept. We have,
$ \Rightarrow 0 = {\left( {x + 5} \right)^2} - 3$
Move 3 on the other side,
$ \Rightarrow {\left( {x + 5} \right)^2} = 3$
Take the square root on both sides,
$ \Rightarrow x + 5 = \pm \sqrt 3 $
Subtract 5 on both sides,
$ \Rightarrow x + 5 - 5 = \pm \sqrt 3 - 5$
Simplify the terms,
$ \Rightarrow x = - 5 \pm \sqrt 3 $
It means the curve cuts the x-axis at $\left( { - 5 + \sqrt 3 ,0} \right)$ and $\left( { - 5 - \sqrt 3 ,0} \right)$.
Let us put $x = 0$ and find the y-intercept. We have,
$ \Rightarrow y = {\left( {0 + 5} \right)^2} - 3$
Simplify the terms,
$ \Rightarrow y = {\left( 5 \right)^2} - 3$
Square the term on the right side,
$ \Rightarrow y = 25 - 3$
Simplify the terms,
$ \Rightarrow y = 22$
It means the curve cuts the y-axis at $\left( {0,22} \right)$.
We know that all quadratic functions of the type $y = a{x^2} + bc + c$ have minimum values but not maximum.
Since the square is always non-negative, we have ${\left( {x + 5} \right)^2} \ge 0$, then we have
$ \Rightarrow y = {\left( {x + 5} \right)^2} - 3 \ge 0$
So, the minimum value of $y = - 3$ and the minimum value occurs when ${\left( {x + 5} \right)^2} = 0$ or $x = - 5$.
We have already three points for the curve $\left( { - 5 - \sqrt 3 ,0} \right)$, $\left( { - 5 + \sqrt 3 ,0} \right)$ and $\left( {0,22} \right)$. We find y for two more points.
At $x = - 5$ we have,
$ \Rightarrow y = {\left( { - 5 + 5} \right)^2} - 3$
Simplify the terms,
$ \Rightarrow y = {\left( 0 \right)^2} - 3$
Simplify the terms,
$ \Rightarrow y = - 3$
At $x = - 2$ we have,
$ \Rightarrow y = {\left( { - 2 + 5} \right)^2} - 3$
Simplify the terms,
$ \Rightarrow y = {\left( 3 \right)^2} - 3$
Square the term on the right side,
$ \Rightarrow y = 9 - 3$
Simplify the terms,
$ \Rightarrow y = 6$
So, we draw the table for x and y.
We plot the above points and join them to have the graph as
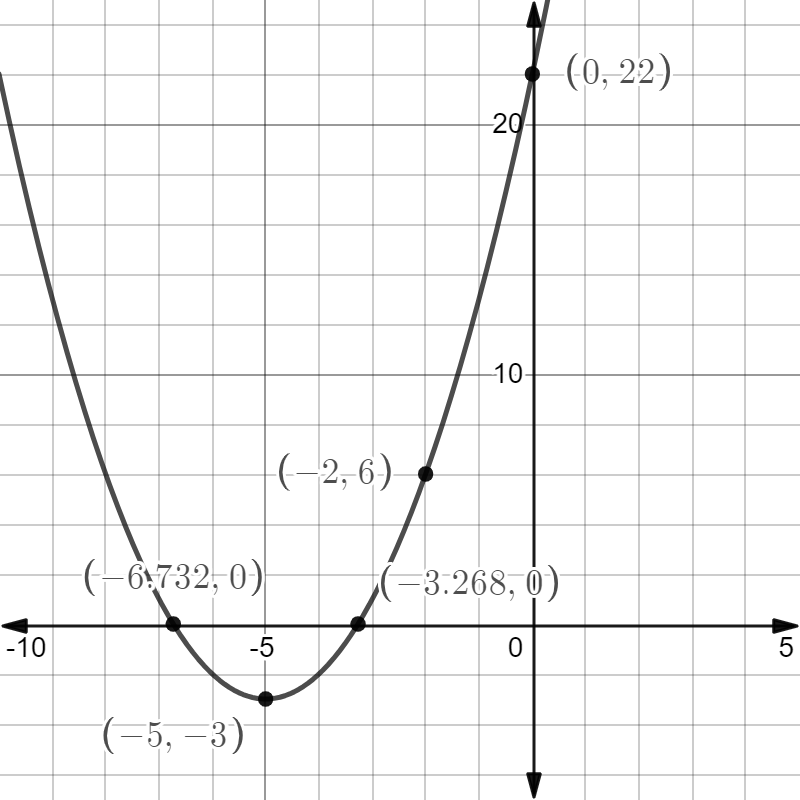
Note: We note that the obtained graph is the graph of the upward parabola whose general equation is given by $y = a{x^2} + bx + c$ with the condition $a > 0$ whose vertex here is $\left( { - 5, - 3} \right)$ . We can directly find the minimum value of $y = {\left( {x + 5} \right)^2} - 3$ by finding $x = - \dfrac{b}{{2a}}$. If $a < 0$ the equation $y = a{x^2} + bx + c$ represents a downward parabola. We also note that the obtained curve is symmetric about the line $x = - 5$.
Complete step by step solution:
We know that the graph of a function is the locus of points $\left( {x,y} \right)$ such that $y = f\left( x \right)$ where x, y are real numbers. We are given the following quadratic polynomial function,
$ \Rightarrow y = {\left( {x + 5} \right)^2} - 3$
So, let us put $y = 0$ and find the x-intercept. We have,
$ \Rightarrow 0 = {\left( {x + 5} \right)^2} - 3$
Move 3 on the other side,
$ \Rightarrow {\left( {x + 5} \right)^2} = 3$
Take the square root on both sides,
$ \Rightarrow x + 5 = \pm \sqrt 3 $
Subtract 5 on both sides,
$ \Rightarrow x + 5 - 5 = \pm \sqrt 3 - 5$
Simplify the terms,
$ \Rightarrow x = - 5 \pm \sqrt 3 $
It means the curve cuts the x-axis at $\left( { - 5 + \sqrt 3 ,0} \right)$ and $\left( { - 5 - \sqrt 3 ,0} \right)$.
Let us put $x = 0$ and find the y-intercept. We have,
$ \Rightarrow y = {\left( {0 + 5} \right)^2} - 3$
Simplify the terms,
$ \Rightarrow y = {\left( 5 \right)^2} - 3$
Square the term on the right side,
$ \Rightarrow y = 25 - 3$
Simplify the terms,
$ \Rightarrow y = 22$
It means the curve cuts the y-axis at $\left( {0,22} \right)$.
We know that all quadratic functions of the type $y = a{x^2} + bc + c$ have minimum values but not maximum.
Since the square is always non-negative, we have ${\left( {x + 5} \right)^2} \ge 0$, then we have
$ \Rightarrow y = {\left( {x + 5} \right)^2} - 3 \ge 0$
So, the minimum value of $y = - 3$ and the minimum value occurs when ${\left( {x + 5} \right)^2} = 0$ or $x = - 5$.
We have already three points for the curve $\left( { - 5 - \sqrt 3 ,0} \right)$, $\left( { - 5 + \sqrt 3 ,0} \right)$ and $\left( {0,22} \right)$. We find y for two more points.
At $x = - 5$ we have,
$ \Rightarrow y = {\left( { - 5 + 5} \right)^2} - 3$
Simplify the terms,
$ \Rightarrow y = {\left( 0 \right)^2} - 3$
Simplify the terms,
$ \Rightarrow y = - 3$
At $x = - 2$ we have,
$ \Rightarrow y = {\left( { - 2 + 5} \right)^2} - 3$
Simplify the terms,
$ \Rightarrow y = {\left( 3 \right)^2} - 3$
Square the term on the right side,
$ \Rightarrow y = 9 - 3$
Simplify the terms,
$ \Rightarrow y = 6$
So, we draw the table for x and y.
| $X$ | $ - 5 - \sqrt 3 $ | $ - 5 + \sqrt 3 $ | $0$ | $-5$ | $-2$ |
| $Y$ | $0$ | $0$ | $22$ | $-3$ | $6$ |
We plot the above points and join them to have the graph as

Note: We note that the obtained graph is the graph of the upward parabola whose general equation is given by $y = a{x^2} + bx + c$ with the condition $a > 0$ whose vertex here is $\left( { - 5, - 3} \right)$ . We can directly find the minimum value of $y = {\left( {x + 5} \right)^2} - 3$ by finding $x = - \dfrac{b}{{2a}}$. If $a < 0$ the equation $y = a{x^2} + bx + c$ represents a downward parabola. We also note that the obtained curve is symmetric about the line $x = - 5$.
Recently Updated Pages
Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Which is the Longest Railway Platform in the world?

India Manned Space Mission Launch Target Month and Year 2025 Update

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the full form of pH?




