Question

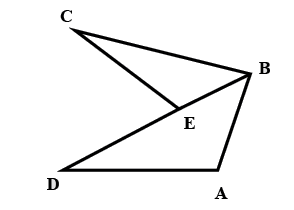
Given\[ED = EC,\]
Then \[AB + AD > BC\]
If the above statement is true, then mention answer as 1, else mention 0 if it is false

Answer 1

Hint: As we know that, in a triangle sum of two sides greater than that of its third side. So, this will help in solving this problem. The Triangle Inequality Theorem states that the sum of any two sides of a triangle must be greater than the measure of the third side. This rule must be satisfied for all 3 conditions of the sides.

Complete step by step solution: Using the Triangle Inequality Theorem, we have a sum of two sides which is always greater than that of its third side. So, the three sides of the triangle should follow this rule,
According to this rule, In\[\vartriangle ABD\],
\[AB + AD > BD\]
\[AB + AD > BE + ED\]--- (1)
Also, in \[\vartriangle BCE\], we have sum of two sides greater than that of its third side
\[BE + EC > BC\]-- (2)
After Adding equations \[1,2\] we get
\[AB + AD + BE + EC > BE + ED + BC\]
Subtracting \[BE\] from both sides
\[AB + AD + EC > ED + BC\]
But it is given for the two sides of the given figure, \[EC = ED\]
So, the two will be cancelled from each side, And we are only left with
Hence, \[AB + AD > BC\]

Note: In a triangle, the sum of two sides can never be less than that of the dimension of its third side. In other words, as soon as you know that the sum of two sides is less than (or equal to) the measure of a third side, then you know that the sides do not make up a triangle.