
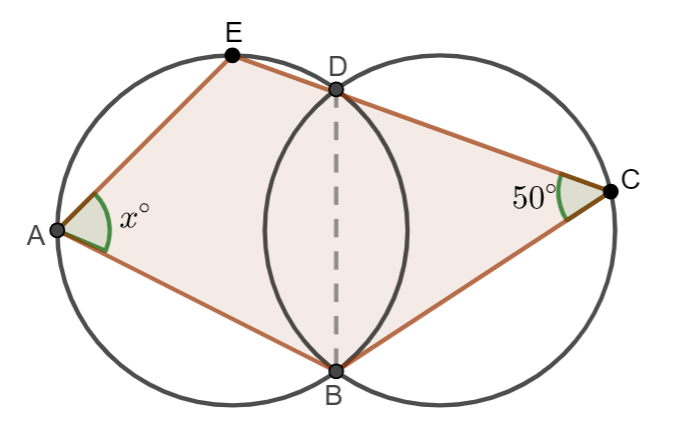
Given that BC = CD, what is the value of x.
A. \[{{50}^{\circ }}\]
B. \[{{55}^{\circ }}\]
C. \[{{60}^{\circ }}\]
D. \[{{65}^{\circ }}\]

Answer
504k+ views
Hint: In this problem, we have to find the value of x in the given diagram. We should first analyse the given diagram. We are also given that BC = CD, whose angle will also be equal. We can then use the angle sum property and find and find the value of one of the angles. We can see that in the first circle AEBD is a cyclic quadrilateral, then the opposite angles will be supplementary, we can use these properties and find the value of the required angle.
Complete step by step answer:
Here we have to find the value of x from the given diagram.
We can see that, in triangle DBC, we are given that \[\angle DCB={{50}^{\circ }}\] and CD = CB, we can now write it as,
\[\Rightarrow \angle CDB=\angle CBD\] …… (1)
By angle sum property, we can write it as,
\[\Rightarrow \angle DCB+\angle DBC+\angle CDB={{180}^{\circ }}\]
From (1), we can write as
\[\begin{align}
& \Rightarrow 2\angle CDB={{180}^{\circ }}-{{50}^{\circ }} \\
& \Rightarrow \angle CDB={{65}^{\circ }}.....(2) \\
\end{align}\]
We can see that, in the first circle AEBD is a cyclic quadrilateral, then opposite angles are supplementary.
We can now write it as,
\[\Rightarrow \angle EAB+\angle EDB={{180}^{\circ }}\]
From the diagram, we can also write the above step as,
\[\begin{align}
& \Rightarrow \angle EAB+{{180}^{\circ }}-\angle CDB={{180}^{\circ }} \\
& \Rightarrow \angle EAB=\angle CDB \\
\end{align}\]
From (2), we can write it as,
\[\Rightarrow \angle EAB=\angle CDB={{65}^{\circ }}\]
The value of x is \[{{65}^{\circ }}\].
Therefore, the answer is option D. \[{{65}^{\circ }}\]
Note: We should always remember that the supplementary angles are angles which sums up to give \[{{180}^{\circ }}\]. We should also know that if the first circle is a cyclic quadrilateral, then opposite angles are supplementary. We should know that angle sum property is the sum of the triangle equals \[{{180}^{\circ }}\].
Complete step by step answer:
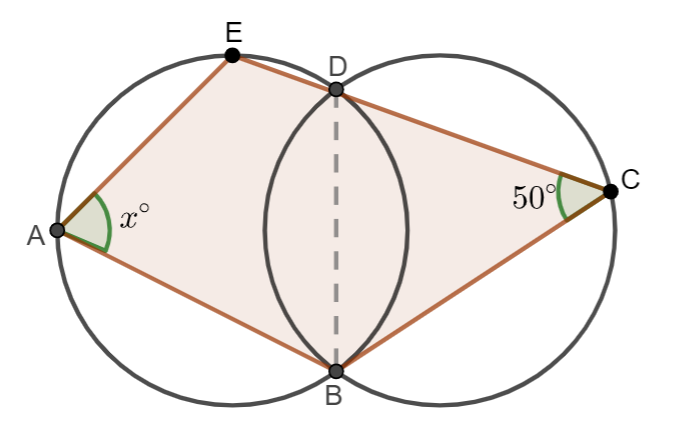
Here we have to find the value of x from the given diagram.

We can see that, in triangle DBC, we are given that \[\angle DCB={{50}^{\circ }}\] and CD = CB, we can now write it as,
\[\Rightarrow \angle CDB=\angle CBD\] …… (1)
By angle sum property, we can write it as,
\[\Rightarrow \angle DCB+\angle DBC+\angle CDB={{180}^{\circ }}\]
From (1), we can write as
\[\begin{align}
& \Rightarrow 2\angle CDB={{180}^{\circ }}-{{50}^{\circ }} \\
& \Rightarrow \angle CDB={{65}^{\circ }}.....(2) \\
\end{align}\]
We can see that, in the first circle AEBD is a cyclic quadrilateral, then opposite angles are supplementary.
We can now write it as,
\[\Rightarrow \angle EAB+\angle EDB={{180}^{\circ }}\]
From the diagram, we can also write the above step as,
\[\begin{align}
& \Rightarrow \angle EAB+{{180}^{\circ }}-\angle CDB={{180}^{\circ }} \\
& \Rightarrow \angle EAB=\angle CDB \\
\end{align}\]
From (2), we can write it as,
\[\Rightarrow \angle EAB=\angle CDB={{65}^{\circ }}\]
The value of x is \[{{65}^{\circ }}\].
Therefore, the answer is option D. \[{{65}^{\circ }}\]
Note: We should always remember that the supplementary angles are angles which sums up to give \[{{180}^{\circ }}\]. We should also know that if the first circle is a cyclic quadrilateral, then opposite angles are supplementary. We should know that angle sum property is the sum of the triangle equals \[{{180}^{\circ }}\].
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




