Question

Give reason for the following: A rectangle can be thought of as a special parallelogram.

Answer 1

Hint: First remember and then write down the properties of rectangle and parallelogram. Then compare them one by one to observe that whose properties are more specified to prove the desired result.

“Complete step-by-step answer:”
We are asked to prove that a rectangle can be thought of as a special parallelogram.
To prove this we have to first write down the properties of parallelogram and rectangle separately.
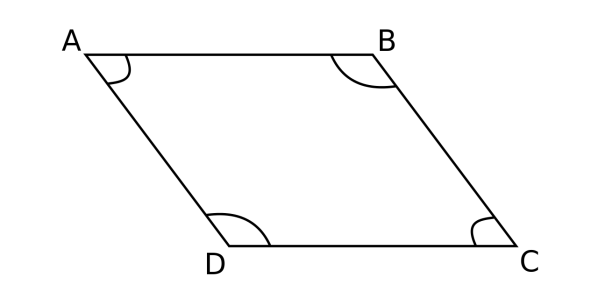
So, the properties of parallelogram are:
i) The opposite sides of a parallelogram are equal and parallel to each other.
ii) Sum of two adjacent angles is ${{180}^{o}}$ .
iii) The diagonals of parallelogram bisect each other equally.
iv) The two pairs of opposite angles are equal to each other.

Now let’s write properties of rectangle are:
i) The opposite sides of the rectangle are equal and parallel to each other.
ii) Each interior angle of the rectangle is ${{90}^{o}}$ .
iii) The diagonals of the rectangle bisect each other equally.
iv) Sum of adjacent angles is ${{180}^{o}}$ and also the opposite pair of angles are equal.

By observing the properties we can tell that either the properties of rectangle and parallelogram are equal or the properties of rectangle are more specified or it’s more pacific than that of parallelogram.
Hence we can say that a rectangle can be thought of as a special parallelogram.
Note: Students must have an idea about the types of special quadrilateral end. They should know the properties of rectangles and parallelograms by heart. They should be well versed with their properties so that they can compare.
Students generally confuse that all rectangles are called as parallelograms or vice versa. So, by comparing their properties also they can say that rectangles are special versions of parallelograms.