Question

From the top of a 7 m high building, the angle of elevation of the top of a cable tower is ${60^0}$ and the angle of depression of its foot is ${45^0}$ . Determine the height of the tower.

Answer 1

Hint- Figure is must in such types of questions. We will use a simple definition of trigonometric angles of a right angled triangle along with the data given. Just as in a right angled triangle tangent of an angle is the length of height upon length of the base of the triangle.

Complete step-by-step solution -

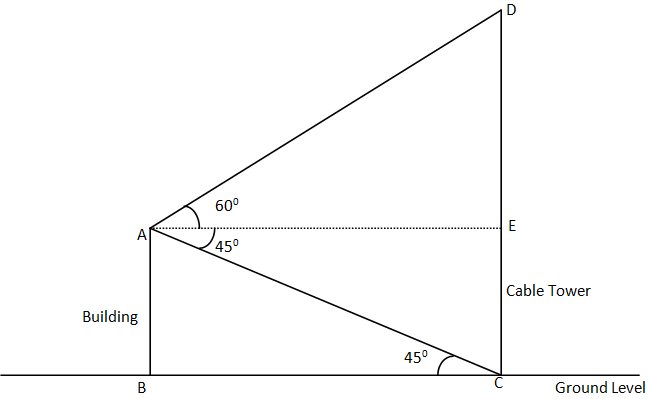
The diagram show above shows the exact model of the data given in the question
AB = Building =7 m (given)
CD = Cable tower
AC = Horizontal line parallel to ground level
As we know that
$\tan \theta = \dfrac{{{\text{perpendicular height}}}}{{{\text{base}}}}$
In order to find AE or correspondingly to find BC, we have:
In $\Delta ABC$
$
  \tan \angle ACB = \dfrac{{AB}}{{BC}} \\
   \Rightarrow \tan {45^0} = \dfrac{{AB}}{{BC}} \\
   \Rightarrow \dfrac{{AB}}{{BC}} = 1\left[ {\because \tan {{45}^0} = 1} \right] \\
   \Rightarrow AB = BC = 7m\left[ {\because AB = 7m({\text{given}})} \right] \\
 $
So we also have
$AE = BC = 7m$
Now in order to find DE we have:
In $\Delta AED$
$
  \tan \angle DAE = \dfrac{{DE}}{{AE}} \\
   \Rightarrow \tan {60^0} = \dfrac{{DE}}{{AE}} \\
   \Rightarrow \dfrac{{DE}}{{AE}} = \sqrt 3 \left[ {\because \tan {{60}^0} = \sqrt 3 } \right] \\
   \Rightarrow DE = AE\left( {\sqrt 3 } \right) = 7\left( {\sqrt 3 } \right)m\left[ {\because AE = 7m({\text{found}})} \right] \\
 $
Now finding the height of the cable tower = CD
\[
   \Rightarrow CD = CE + DE \\
   \Rightarrow CD = AB + DE\left[ {\because CE = AB} \right] \\
   \Rightarrow CD = 7m + 7\sqrt 3 m \\
   \Rightarrow CD = 7\left( {1 + \sqrt 3 } \right)m \\
   \Rightarrow CD = 7\left( {1 + 1.732} \right)m\left[ {\because \sqrt 3 = 1.732} \right] \\
   \Rightarrow CD = 7\left( {2.732} \right)m \\
   \Rightarrow CD = 19.124m \\
 \]
Hence, the height of the cable tower is 19.124 m.

Note- In order to solve such kinds of questions related to practical application of heights and distances figures play a major role in easier simplification of the problem. If this question was not solved by figures, it could be very hectic to solve though. Always remember the values of trigonometric functions of some special angles, two of them are mentioned above. Try to solve the problem in parts.