Question

Four pipes each of 5cm in diameter are to be replaced by a single pipe discharging the same quantity of water. If the speed of water remains same in both the cases, then the diameter (in cm) of the single pipe is
(a) $5$
(b) $6$
(c) $10$
(d) $12$

Answer 1

Hint: The four pipes each of diameter $5cm$ get replaced by a single pipe which discharges the same amount of water. This means that the volume of that single pipe must be equal to the sum of the volumes of the four pipes. Since a pipe is cylindrical in shape, so the volume of a pipe can be found by using the formula of the volume of a cylinder, which is given by $V=\pi {{r}^{2}}h$ where $r$ and $h$ are respectively the radius and the height of the cylinder. So on equating the volume of the cylinder with the total volume of the four cylinders, we will get the required diameter of the single pipe.

Complete step by step solution:
Let the length of each of the four pipes be $l$. So these pipes can be shown in the below figure as

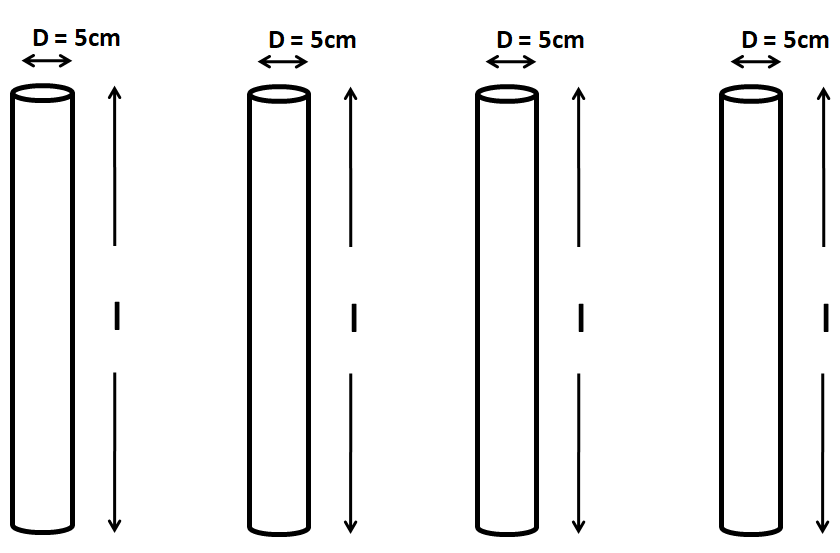
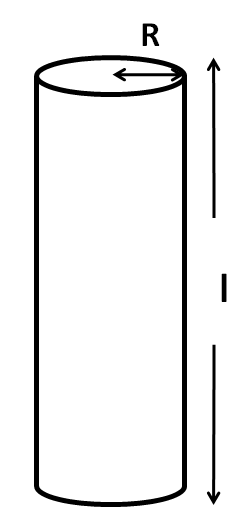
Also, these pipes are replaced by a single pipe, as shown in the below figure.

The diameter of each of the pipes is given to be equal to $5cm$. So we have
$\Rightarrow D=5cm........(i)$
Now, since a pipe is cylindrical in shape, so the volume of each of the pipes is given by
$\Rightarrow V=\pi {{r}^{2}}l$
Now, we know that the radius is equal to half of the diameter. So we can write
\[\begin{align}
  & \Rightarrow V=\pi {{\left( \dfrac{D}{2} \right)}^{2}}l \\
 & \Rightarrow V=\dfrac{\pi {{D}^{2}}l}{4}........(ii) \\
\end{align}\]
Now, according to the question the four pipes are replaced with a single pipe which supplies the same quantity of water as the four pipes. This means that the volume of the single pipe $\left( {{V}_{S}} \right)$ must be equal to the total volume of the four pipes, that is
\[\Rightarrow {{V}_{S}}=4V.........(iii)\]
If the radius and the length of the pipe are $R$ and $l$ respectively, then we have
$\Rightarrow {{V}_{S}}=\pi {{R}^{2}}l.........(iv)$
From (iv) and (v) we have
\[\Rightarrow \pi {{R}^{2}}l=4V\]
Putting (ii) in the above equation, we get
$\begin{align}
  & \Rightarrow \pi {{R}^{2}}l=4\left( \dfrac{\pi {{D}^{2}}l}{4} \right) \\
 & \Rightarrow \pi {{R}^{2}}l=\pi {{D}^{2}}l \\
\end{align}$
Cancelling $\pi l$ from both the sides
$\begin{align}
  & \Rightarrow {{R}^{2}}={{D}^{2}} \\
 & \Rightarrow R=D \\
\end{align}$
From (i)
$\Rightarrow R=5cm$
Since the diameter is the twice the radius, so the diameter of the single pipe is
$\begin{align}
  & \Rightarrow D=2R \\
 & \Rightarrow D=2\times 5cm \\
 & \Rightarrow D=10cm \\
\end{align}$
Hence, the correct answer is option (c).

Note: In the above question, we have been asked the value of the diameter of the single pipe, and not its radius. So do not forget to obtain the diameter of the single pipe from the value of the radius. Also, the information regarding the speed given in this problem is immaterial to the solution. So do not get confused by the same. Also, we must remember the formula for the volume of a cylinder, which is given by $V=\pi {{r}^{2}}h$. In case we forget it, we can easily derive it by multiplying the area of the circular base with the height.