Question

For the reaction,
 \[SO_2\left( g \right){\text{ }} + {\text{ }}NO_2\left( g \right)\;\; \rightleftharpoons \;SO_3\left( g \right){\text{ }} + {\text{ }}NO\left( g \right)\;\] \[Kc{\text{ }} = {\text{ }}16\].
The reaction is carried out in a closed container at a fixed temperature. Find the concentration of \[NO\] and \[N{O_2}\] at equilibrium if \[1{\text{ }}mol\]of each reacts in a container of \[1{\text{ }}liter\] capacity.

Answer 1

Hint: We have to find the concentration of \[NO\]and at equilibrium. So we can use the equilibrium constant formula to solve the problem,
\[Kc = \dfrac{{{{\left[ C \right]}^c}{{\left[ D \right]}^d}}}{{{{\left[ A \right]}^a}{{\left[ B \right]}^b}}}\]

Complete step by step solution:
We can define the equilibrium constant \[(Kc)\]is the ratio of the equilibrium concentrations of products upon the equilibrium concentrations of reactants and that each reactant and product raised to the power of their respective coefficients.
 Thus,the equilibrium constant,\[Kc\] , for the reaction \[{\text{aA + bB }} \rightleftharpoons {\text{ cC + dD}}\] is given as,
\[Kc{\text{ }} = \]\[\dfrac{{{{\left[ C \right]}^c}{{\left[ D \right]}^d}}}{{{{\left[ A \right]}^a}{{\left[ B \right]}^b}}}\]
where A and B are reactants and C &D are products. a,b,c and d are their coefficients respectively.
Given,
Volume Of container = \[1{\text{ }}Liter\]
Equilibriumconstant = \[Kc{\text{ }} = {\text{ }}16\]
The equilibrium reaction is \[{\text{SO_2}}\left( {\text{g}} \right){\text{ + NO_2}}\left( {\text{g}} \right){\text{}} \rightleftharpoons {\text{SO_3}}\left( {\text{g}} \right){\text{ + NO}}\left( {\text{g}} \right){\text{}}\]
of each of the four gases given is \[1{\text{ }}M\]each,then

	\[S{O_2}\]	\[N{O_2}\]	\[S{O_3}\]	\[NO\]
The initial concentrations	\[1M\]	\[1M\]	\[1M\]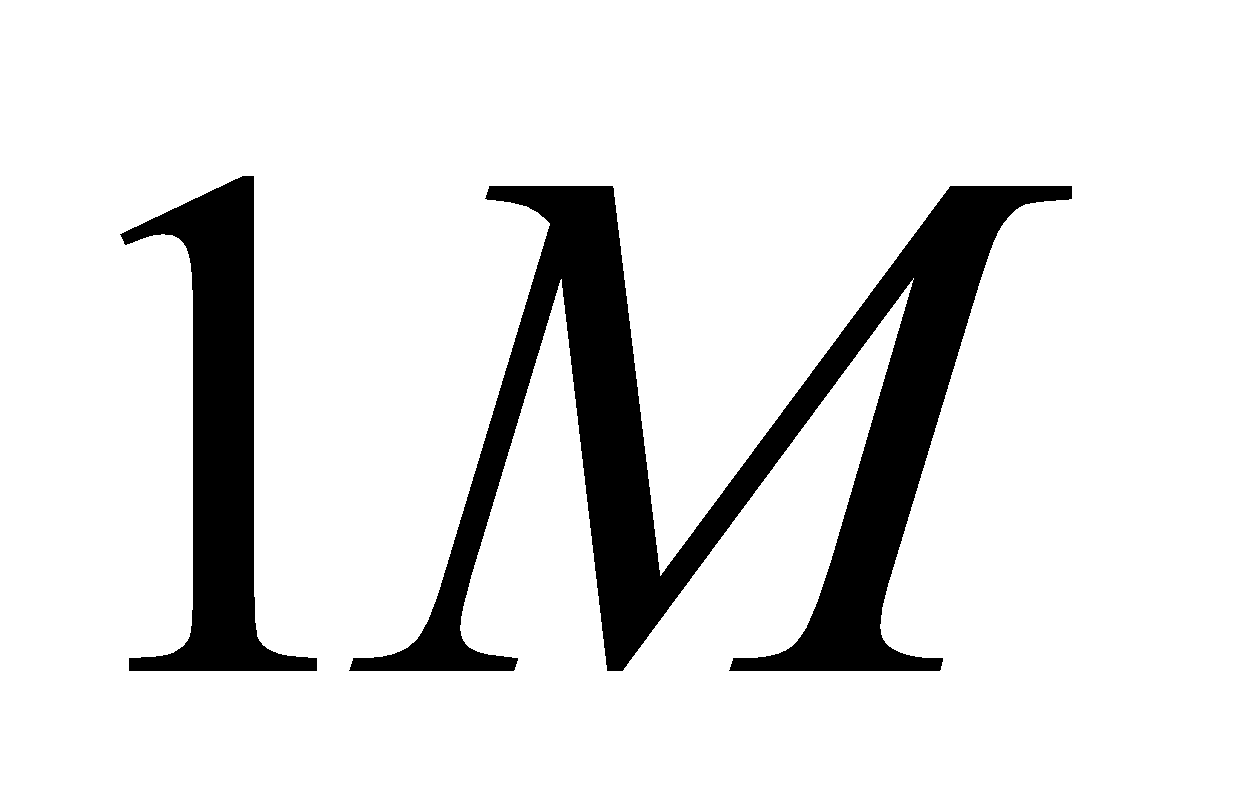
The equilibrium concentrations	\[\left( {1 - x} \right)M\]	\[\left( {1 - x} \right)M\]	\[\left( {1 + x} \right)M\]	\[\left( {1 + x} \right)M\]

Now, by applying the formula for the expression for the equilibrium constant,

\[Kc = \]\[\dfrac{{{{\left[ {SO_3} \right]}^{}}{{\left[ {NO} \right]}^{}}}}{{{{\left[ {SO_2} \right]}^{}}{{\left[ {NO_2} \right]}^{}}}}\]
Putting the values of equilibrium concentrations of reactants and products ,we get
\[Kc = \] \[\dfrac{{\left[ {1 + x} \right]\left[ {1 + x} \right]}}{{\left[ {1 - x} \right]\left[ {1 - x} \right]}}\] As \[Kc\] is 16 , then by solving the above we get,
∴ \[16 = \dfrac{{{{\left( {1 + x} \right)}^2}}}{{{{\left( {1 - x} \right)}^2}}}\]
∴ ​\[4 = \dfrac{{\left( {1 + x} \right)}}{{\left( {1 - x} \right)}}\] after simplifying above
∴ \[x{\text{ }} = {\text{ }}0.6\] By substituting the value of x ,
\[\left[ {S{O_3}} \right]{\text{ }} = {\text{ }}\left[ {NO} \right]{\text{ }} = {\text{ }}\left( {1 + {\text{ }}x} \right){\text{ }} = {\text{ }}1 + 0.6{\text{ }} = {\text{ }}1.6{\text{ }}mol/L\]
\[\left[ {S{O_2}} \right]{\text{ }} = {\text{ }}\left[ {N{O_2}} \right]{\text{ }} = {\text{ }}\left( {1 - {\text{ }}x} \right){\text{ }} = {\text{ }}1{\text{ }} - {\text{ }}0.6{\text{ }} = {\text{ }}0.4{\text{ }}mol/L\]

Hence, the concentration of \[N{O_2}\] and \[NO\] are\[\;0.4{\text{ }}mol/L\] and \[1.6{\text{ }}mol/L\]respectively.

Note: We can use equilibrium constant (Kc) to determine the extent of a reaction.therefore, the degree of the disappearance of the reactants. The magnitude of the equilibrium constant gives a knowledge of the relative amount of the reactants and the products in an equilibrium reaction.