Question

For a concave mirror of focal length f, image is at distance 2 times of focal length. Find the magnitude of object distance.
A. f
B. 2f
C. 3f
D. 4f

Answer 1

Hint: To solve this kind of problem, we need to have the knowledge of the relations between the object distance, image distance and focal length relations for both concave mirror and convex mirror. The mirror formula for the concave mirror is: $\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$, while for a convex mirror it is: $\dfrac{1}{u}-\dfrac{1}{v}=\dfrac{-1}{f}.$ Making a ray diagram of the problem will help with understanding the problem.

Step by step solution:
Let’s start by taking a general case. An object is kept at point B in the principal axis. Three rays emerge from it, as shown in the diagram below. The ray going parallel to the principal axis hits the mirror at M. The reflected ray will cut the principal axis at the focus of the mirror at point F. Another ray emerging from the object hits the mirror at the center of the mirror, where the principal axis cuts the mirror as well at point P. This ray gets reflected back and again converges with the reflected ray at point ${A}'$. Another ray emerging from the object directly passes through the point ${A}'$ hitting the mirror at point N. Hence the mirror image forms at point ${B}'.$

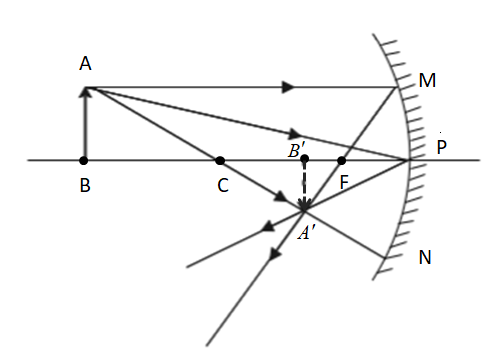
From the diagram we can find two right angled triangles ${A}'{B}'F$ and MPF respectively. Here, we consider paraxial rays, for which MP is perpendicular to CP.

Therefore,$\dfrac{{B}'{A}'}{PM}=\dfrac{{B}'F}{FP}\Rightarrow \dfrac{{B}'{A}'}{BA}=\dfrac{{B}'F}{FP}(\because PM=AB)\to (1)$
 The triangles ${A}'{B}'P$ and ABP are also similar right angled triangles.
Therefore, $\dfrac{{B}'{A}'}{BA}=\dfrac{{B}'P}{BP}\to (2)$

Comparing the above two equations, we get, $\dfrac{{B}'F}{FP}=\dfrac{{B}'P-FP}{FP}=\dfrac{{B}'{A}'}{BP}\to (3)$

To convert these distances into object distance (u), image distance (v) and focal length (f) we need to first consider the direction of the ray.
Hence, ${B}'P=-v,FP=-f,BP=-u$
Substituting these values into the equation 3, we get,$\dfrac{-v+f}{-f}=\dfrac{-v}{-u}\Rightarrow \dfrac{v-f}{f}=\dfrac{v}{u}$

That is,$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}\to (4)$ for a concave mirror.
Hence, putting in the condition as stated in the problem into equation 4, (v=2f)
Therefore, $\dfrac{1}{u}+\dfrac{1}{2f}=\dfrac{1}{f}\Rightarrow \dfrac{1}{u}=\dfrac{2-1}{2f}\Rightarrow u=2f$

Hence, the object distance is 2f.

Note:
If you get confused between concave and convex mirrors, you can remember that a concave mirror has a ‘cave’ in it. Hence, the mirror’s reflecting side caves in hence, it’s a converging mirror.
Alternatively, a convex mirror is also known as a diverging mirror, which means that, when parallel rays hit the convex mirror, they diverge away. Here, the reflecting side is bulging out.