Questions & Answers
Question
AnswersFind three solutions different solution of the equation
y = 6x.
Answer
Verified130.2k+ views
Hint: In order to solve this problem, we need to plot any three points that satisfy this equation. For this, we can start by assuming any three values of x and then get the three values of y coordinates. With these three points, we can even plot the graph of the line y = 6x.
Complete step-by-step solution:
We have been given the equation $y = 6x$.
And we need to find any three solutions to this equation.
Let try to get the insight into how this equation looks.
Every point on the line satisfies this equation of the line.
Hence, we can start by plotting be considering any two points.
We need at least two points to plot the line on a plane.
Let’s consider the simplest point.
Let substitute, $x = 0$, we get,
$y = (0)\times6$
$y = 0$
Hence, the point it passes is (0,0).
Let this point be O (0,0).
Moving on let’s substitute $x = 1$, we get,
$y = (1) \times 6$
$y = 6$
Hence, the point it passes is (1,6).
Let this point be A (1,6).
With two points we can plot the line of $y = 6x$.
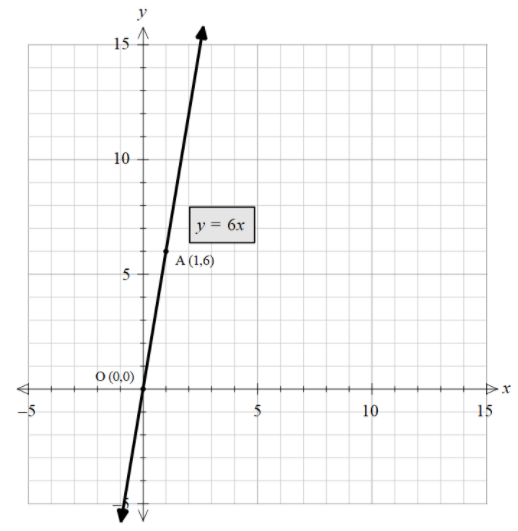
Now, we can plot any point by looking at the graph or just by substituting values in the equation.
Moving on let’s substitute $x = 2$, we get,
$y = (2) \times 6$
$y = 12$
Hence, the point it passes is (2,12).
Let this point be B (2,12).
Moving on let’s substitute $x = 3$, we get,
$y = (3) \times 6$
$y = 18$
Hence, the point it passes is (3,18).
Let this point be C (3,18).
Hence, the three solutions of the equations are A (1,6), B (2,12), and C (3,18).
Note: We can solve this by another approach we can plot the equation by considering any two-point and by looking at the graph we can plot the third equation. Also, we can see in the solution the ‘y’ coordinate is 6 times the x coordinates. This is what exactly the equation tells us. We can use this technique to check whether the point lies on the line or not.
Complete step-by-step solution:
We have been given the equation $y = 6x$.
And we need to find any three solutions to this equation.
Let try to get the insight into how this equation looks.
Every point on the line satisfies this equation of the line.
Hence, we can start by plotting be considering any two points.
We need at least two points to plot the line on a plane.
Let’s consider the simplest point.
Let substitute, $x = 0$, we get,
$y = (0)\times6$
$y = 0$
Hence, the point it passes is (0,0).
Let this point be O (0,0).
Moving on let’s substitute $x = 1$, we get,
$y = (1) \times 6$
$y = 6$
Hence, the point it passes is (1,6).
Let this point be A (1,6).
With two points we can plot the line of $y = 6x$.
Now, we can plot any point by looking at the graph or just by substituting values in the equation.
Moving on let’s substitute $x = 2$, we get,
$y = (2) \times 6$
$y = 12$
Hence, the point it passes is (2,12).
Let this point be B (2,12).
Moving on let’s substitute $x = 3$, we get,
$y = (3) \times 6$
$y = 18$
Hence, the point it passes is (3,18).
Let this point be C (3,18).
Hence, the three solutions of the equations are A (1,6), B (2,12), and C (3,18).
Note: We can solve this by another approach we can plot the equation by considering any two-point and by looking at the graph we can plot the third equation. Also, we can see in the solution the ‘y’ coordinate is 6 times the x coordinates. This is what exactly the equation tells us. We can use this technique to check whether the point lies on the line or not.