Question

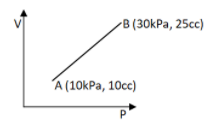
Find the work done for the process shown in the figure

(a) 1J
(b) 1.5J
(c) 4.5J
(d) 0.3J

Answer 1

Hint: The work done of the process is found by calculating the area under the curve. Redraw the diagram and extend lines to the X and Y axis from points A and B. Calculate the total area by dividing it into smaller areas. In this figure divide it into a triangular and rectangular area and then sum the values of the area. The total area will give the work done.

Formula used: \[Area{\text{ }}of{\text{ }}rectangle = {\text{ }}length{\text{ }}x{\text{ }}breadth\] ; \[Area{\text{ }}of{\text{ }}triangle{\text{ }} = \;\dfrac{1}{2}*{\text{ }}Base{\text{ * }}height\]

Complete step-by-step solution:

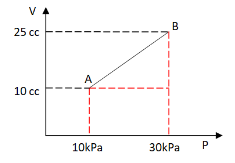
\[P - {\text{ }}Pressure\]
\[Pa - {\text{ }}Pascal{\text{ }}(Unit{\text{ }}of{\text{ }}pressure)\]
\[V - {\text{ }}Volume\]
\[cc - {\text{ }}cubic{\text{ }}centimeter{\text{ }}\left( {Unit{\text{ }}of{\text{ }}volume} \right)\]
The work done is calculated by summing the area under the line AB. So from the diagram, the sum of the area (area 0f the rectangle + area of the triangle) will give the work done for the process.
Given: Initial volume =\[10{\text{ }}cc\] ; Final volume = \[25{\text{ }}cc\]
Initial Pressure =\[10kPa\] ; Final pressure = \[30kPa\]
To find: work done
Area of the rectangle (from the diagram) = Length x breadth
Substituting the values, = \[\left( {30 - 10} \right){\text{* }}10\]
\[ = {\text{ }}20{\text{ * }}10\]
\[Area{\text{ }}of{\text{ }}rectangle\;\;\; = {\text{ }}200kPa.cc\]
Area of the triangle (from the diagram) = \[\;\dfrac{1}{2}{\text{* }}Base{\text{ * }}height\]
\[ = \;\dfrac{1}{2}*{\text{ }}10{\text{ * }}20\]
Simplifying, Area of triangle= \[100\] kPa.cc
The work done is the sum of the area,
Therefore, Work done= Area of rectangle + Area of triangle
Substituting the values, = \[200\] kPa.cc + \[100\] kPa.cc
Adding,= \[300\] kPa.cc
To convert cubic centimeter to cubic meter, multiply by \[{10^{ - 6}}\] (1 cubic centimeter= \[{10^{ - 6}}\] cubic meter)
Therefore, Work done = \[300{\text{ * }}{10^{ - 6}}\] kPa.m3
Since \[kPa = {\text{ }}1000\] Pa and multiplying, Work done= \[0.3\] Pa.m3
Since\[Pa.{m^3} = {\text{ }}J\] , Work done=\[0.3\]J (J- Joules)
Hence option (D) W= \[0.3\]J is the right answer.

Note: The energy that is utilized to move an object against force is called work. The work done by a gas depends on both the initial and final state of a gas. For a pressure-volume graph, the area under the curve gives the work done by the gas.