
Find the volume of the largest right circular cone that can be cut out of a cube whose edge is 9 cm.
Answer
606.9k+ views
Hint: The largest circular cone that can be cut out of the cube will have height equal to cube edge and base diameter of cone will be equal to edge of the cube.
Largest right circular cone will have the same height. Let this height be h.
Diameter of the base of the cone is equal to the edge of the cube since it touches all the edges of the cube side.
Let the radius be r.
$ \Rightarrow h = 9cm\;\& \;r = \dfrac{{diameter}}{2} = \dfrac{9}{2} = 4.5cm$
We know that volume of a cone with radius r and height h is
Volume $ = \dfrac{1}{3}\pi {r^2}h$
Substituting r and h values in the above formula, we get
$ \Rightarrow Volume = \dfrac{1}{3}\pi {\left( {4.5} \right)^2}9 = 190.85c{m^3}$
$\therefore $ The volume of the largest right circular cone formed from the given cube is $190.85c{m^3}$
Note:
Here the base of the cone will be the circle inscribed in the face of the cube and its height will be equal to the edge length of the cube. We need to visualize the given problem in geometrical structures to solve the problem easily. When we represent the given problem in graphical form it looks similar to the below figure.
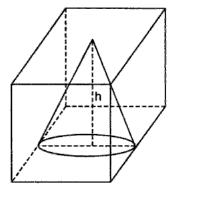
Largest right circular cone will have the same height. Let this height be h.
Diameter of the base of the cone is equal to the edge of the cube since it touches all the edges of the cube side.
Let the radius be r.
$ \Rightarrow h = 9cm\;\& \;r = \dfrac{{diameter}}{2} = \dfrac{9}{2} = 4.5cm$
We know that volume of a cone with radius r and height h is
Volume $ = \dfrac{1}{3}\pi {r^2}h$
Substituting r and h values in the above formula, we get
$ \Rightarrow Volume = \dfrac{1}{3}\pi {\left( {4.5} \right)^2}9 = 190.85c{m^3}$
$\therefore $ The volume of the largest right circular cone formed from the given cube is $190.85c{m^3}$
Note:
Here the base of the cone will be the circle inscribed in the face of the cube and its height will be equal to the edge length of the cube. We need to visualize the given problem in geometrical structures to solve the problem easily. When we represent the given problem in graphical form it looks similar to the below figure.

Recently Updated Pages
Noncooperation programme was adopted by congress at class 10 social science CBSE

A man travels 370km partly by train and partly by car class 10 maths CBSE

A heap of wheat is in the form of a cone whose dia-class-10-maths-CBSE

Through the vertex O of the parabola y24ax two chords class 10 maths CBSE

Find the area of the triangle formed by the points class 10 maths CBSE

What is fallow land Give two examples showing how it class 10 social science CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




