Question

Find the values of other five trigonometric ratios;
\[\sin x = \dfrac{3}{5}\], x lies in the second quadrant.

Answer 1

Hint:
Proceed with the basic definition of given trigonometric ratios and from that we are able to get the idea about the sides of the triangle as if two sides are known then the third side can be calculated using Pythagoras theorem. Hence, knowing the length of all three sides we can obtain various other trigonometric ratios. Also, considering the sign conventions that in the first quadrant all are positive, in the second quadrant sine, cosecant are positive, in third quadrant tangent and cotangent are positive and in the fourth quadrant cosine and secant are positive. And hence considering all these we can obtain our required answer.

Complete step by step solution:
As the given trigonometric ratio is \[\sin x = \dfrac{3}{5}\]
And so in second quadrant we know that only sine and cosecant are positive while all other trigonometric ratios are negative.
Hence, now making triangle in order to get lengths of all sides as,
Diagram:

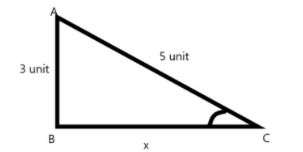
Using Pythagoras theorem calculating the value of x,
Using \[AC = \sqrt {A{B^2} + B{C^2}} \]
On squaring both sides \[A{C^2} = A{B^2} + B{C^2}\]
Now putting the length of side in above equation we can calculate x as,
\[ \Rightarrow \]\[{(5)^2} = {x^2} + {(3)^2}\]
On solving above equation we get,
\[ \Rightarrow \]\[{(x)^2} = 25 - 9\]
On simplifying we get,
\[ \Rightarrow \]\[{(x)^2} = 16\]
Hence, on taking square root,
\[ \Rightarrow \]\[x = 4\,unit\]
Now, as all the side lengths are known we can calculate all trigonometric ratios using proper convention as,
\[ \Rightarrow \]\[\cos x = \dfrac{{adj.}}{{hypo.}} = - \dfrac{4}{5}\]
On calculating other ratio as,
\[ \Rightarrow \]\[\tan x = \dfrac{{opp.}}{{adj.}} = - \dfrac{3}{4}\]
As we know that cosecant, secant and cotangent are inverse of sine, cosine and tangent hence on taking their ratios we get,
\[ \Rightarrow \]\[\cos ecx = \dfrac{{hypo.}}{{opp.}} = \dfrac{5}{3}\]
On calculating another ratio we get,
\[ \Rightarrow \]\[secx = \dfrac{{hypo.}}{{adj.}} = - \dfrac{5}{4}\]
And calculating another ratio we get,
\[ \Rightarrow \]\[\cot x = \dfrac{{adj.}}{{opp.}} = - \dfrac{4}{3}\]

Hence, all the required ratios are calculated.

Note:
There are six trigonometric ratios, sine, cosine, tangent, cosecant, secant and cotangent. These six trigonometric ratios are abbreviated as sin, cos, tan, csc, sec, cot. These are referred to as ratios since they can be expressed in terms of the sides of a right-angled triangle for a specific angle x.
Apply Pythagoras theorem carefully and also draw and calculate the triangle and sides of the triangle without any mistake.
In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others.