Question

Find the value of x in the given figure.

Answer 1

Hint: In this question we have to find the value of x. In order to find x we will use the trigonometric formula, $\cos x = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}$. This will help us reach the answer.

Complete step-by-step answer:
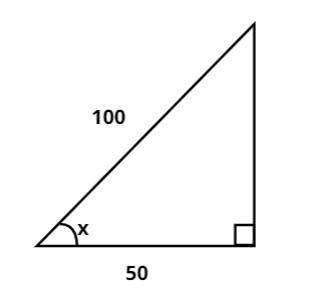
From the given figure we can say that,

Base = 50 and Hypotenuse=100

So, to find x we can use the cosine formula, that is $\cos x = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}$

$ \Rightarrow \cos x = \dfrac{{50}}{{100}}$

$ \Rightarrow \cos x = \dfrac{1}{2}$

Now, as we know that $\cos {60^0} = \dfrac{1}{2}$. Therefore,

x = $60^o$

Note: Whenever we face such types of problems the main point to remember is that we need to have a good grasp over trigonometric properties, some of which have been used above. We must also remember the value of cosines of some common values to use them whenever required. This helps in getting us the required condition and gets us on the right track to reach the answer.