Question

How do you find the third angle of a triangle given $130{}^\circ $, $27{}^\circ $?

Answer 1

Hint: In this problem we have the two angles of a triangle and asked to calculate the third one. So, we will assume the third angle as $x$. First thing we need to know is a triangle is a polygon which has $3$ sides and $3$ interior angles. We know that the sum of the interior angles in a polygon is given by $\left( n-2 \right)\times 180{}^\circ $ where $n$ is the number of sides in the polygon. From this we will calculate the sum of the interior angles of the triangle. Now we will calculate the sum of the interior angles from the data we have. Now we will get an equation to calculate the required result. After solving the obtained equation, we will get our required result.

Complete step-by-step solution:
Given, the two interior angles of the triangle are $130{}^\circ $, $27{}^\circ $.
Let the third angle of the triangle is $x$.
We know that the triangle is a polygon which is having $3$ sides and $3$ interior angles. Now the sum of the three interior angles of the triangle is given by
$\begin{align}
  & s=\left( n-2 \right)\times 180{}^\circ \\
 & \Rightarrow s=\left( 3-2 \right)\times 180{}^\circ \\
 & \Rightarrow s=180{}^\circ \\
\end{align}$
Now the sum of the interior angles of the given triangle is
$s=130{}^\circ +27{}^\circ +x$
We have the sum as $s=180{}^\circ $, then
$\Rightarrow 130{}^\circ +27{}^\circ +x=180{}^\circ $
Simplifying the above equation, then we will get
$\Rightarrow 157{}^\circ +x=180{}^\circ $
Subtracting $157{}^\circ $ on both sides of the above equation, then we will get
$\Rightarrow 157{}^\circ +x-157{}^\circ =180{}^\circ -157{}^\circ $
Simplifying the above equation, then we will have
$\Rightarrow x=23{}^\circ $
Hence the third angle of the given triangle is $23{}^\circ $. The typical diagram of the triangle is also given as

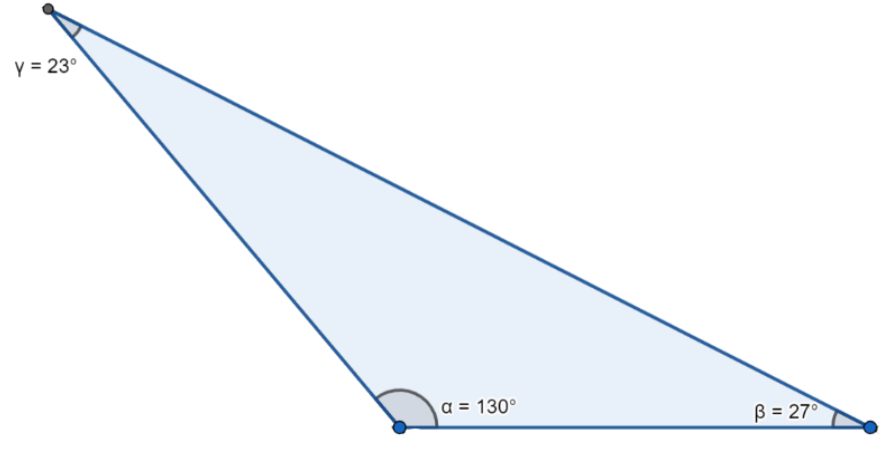
Note: In this problem they have mentioned that the polygon is a triangle, so we have followed the above method. In some cases, they will go with different kinds of polygons like rectangle, pentagon etc., in those cases also the above-mentioned procedure is followed to get the required result.