Question

Find the reflection of the point $( - 3, - 2)$ in y-axis.

Answer 1

Hint:When a point is reflected on y—axis it means that the value of its x coordinate will become the negative of its actual value while the valueof the y coordinate will stay the same. Hence when a point (x, y) is reflected in the y-axis, then it will become (-x, y) upon reflection.


Complete step by step solution:
In the question, the point given to us is $( - 3, - 2)$ , and we need to find the coordinates after it is reflected in the y-axis. The point $( - 3, - 2)$ lies in the third quadrant with 3 units along the negative x axis and 2 units along the negative y-axis.
As per the rule of reflection of points in the y-axis, the x coordinate will become negative of its value while the y coordinate will stay the same.
Let the points $( - 3, - 2)$ be $( - x, - y)$ .
Then according to the rule of reflection y-axis, $( - x, - y)$ upon reflection in y-axis will now become $( - ( - x), - y) = (x, - y)$ , that is, the x coordinate will become positive while the y coordinate will stay negative.
So putting $( - 3, - 2)$ in $( - x, - y)$, the point $( - 3, - 2)$upon reflection in y-axis will become $( - ( - 3), - 2) = (3, - 2)$, that is it will now lie in the fourth quadrant at 3 units along the positive x-axis and 2 units along the negative y-axis.

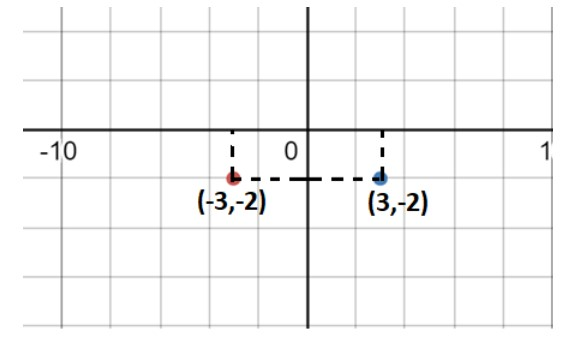
Therefore the point $( - 3, - 2)$ will become $(3, - 2)$ upon reflection in y-axis.


Note: For a point reflected in x-axis, the x coordinate stays the same while the y coordinate becomes the negative of its value. A point $(x,y)$ will become $(x, - y)$ upon reflection in x-axis. For a point reflected in origin, both the x coordinate and y coordinate become negative of its values. A point $(x,y)$ will become $( - x, - y)$ when reflected along the origin $(0,0)$.