Question

Find the number of roots of the equation: ${e^{x - 1}} + x - 2 = 0$.
A. One real root
B. Two real roots
C. Three real roots
D. Four real roots

Answer 1

Hint: We see that we have a function with exponential function. So, we cannot hop on it directly. We will try to use the method of finding the derivative to know the function is strictly increasing or decreasing so that we have only one real root or accordingly.

Complete step-by-step answer:
Let us denote the function given to us by $f(x)$.
So, $f(x) = {e^{x - 1}} + x - 2$.
Now, we will find its derivative.
So, we will get:-
$f'(x) = \dfrac{d}{{dx}}({e^{x - 1}}) \times \dfrac{d}{{dx}}(x - 1) + \dfrac{d}{{dx}}(x)$ ……(1)
We know that $\dfrac{d}{{dx}}({e^x}) = {e^x}$ and $\dfrac{d}{{dx}}({x^n}) = {x^{n - 1}}$.
Using these formulas in (1), we will have with us:-
$f'(x) = {e^{x - 1}} \times 1 + 1$
$\therefore f'(x) = {e^{x - 1}} + 1$ ……..(1)
Now, let us draw the graph of ${e^{x - 1}}$ to know about the range of values it can possess.
     

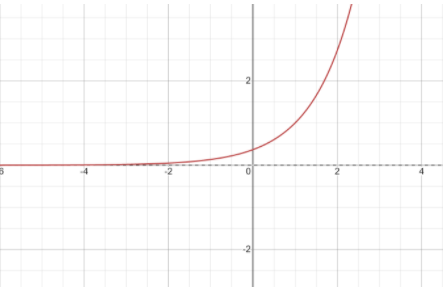
We clearly see from the graph that it never takes negative value.
So, ${e^{x - 1}} > 0$.
Hence, by putting this in (1), we have:
$\therefore f'(x) = {e^{x - 1}} + 1 > 0 + 1 = 1$.
Hence, $f(x)$ is strictly increasing.
We must carefully observe now that if a graph just keeps on increasing for increasing values of x, we can never have more than one point where the graph touches the x- axis.
The point where the graph touches the x- axis is called the real root of the graph.
Hence, we can have one real root.

Note: The students might use the same trick in any other question as well but forget that we need strictly increasing graphs. $\therefore f'(x) > 0$ can work only, not $f'(x) \geqslant 0$ because then there might be more than one root.
The students also might get confused that if it does follow the strictly increasing condition, then it definitely has one real root, but that is not true. This is just a necessary condition not a sufficient one. Example to prove this is take the graph of $y = x$, where $x > 1$. We will have:-
     

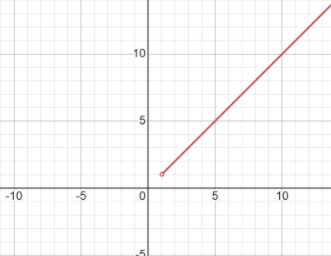
Here, we have all the conditions as per we had in the above solved question. Our derivative is strictly increasing.
But, this does not have any real root because $y \ne 0$ for any value of $x$.