Question

Find the number of diagonals in a Decagon.

Answer 1

Hint: As the name suggests decagon, it has 10 edges and 10 vertices,
Basically, the idea to find the number of diagonals is, as we know that diagonal is formed by joining two vertices of any polygon so using some basic permutation, we can find total number of diagonals
Possibility for that vertices to join another vertex to form a diagonal is \[10-3=7\]

Complete step-by-step answer:

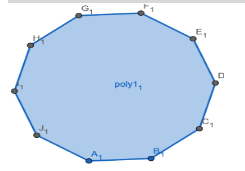
In this Decagon we can clearly see that that point \[{{A}_{1}}\] has \[10-3=7\] point for making a diagonal
We counted 10 because total 10 vertices but
we subtract 3 points which are \[{{A}_{1}},{{J}_{1}},{{B}_{1}}\] out of 10 points because these three points are connected from their respective edge.
So total 7 diagonals are \[{{A}_{1}}{{C}_{1}},{{A}_{1}}{{D}_{1}},{{A}_{1}}{{E}_{1}},{{A}_{1}}{{F}_{1}},{{A}_{1}}{{G}_{1}},{{A}_{1}}{{H}_{1}},{{A}_{1}}{{I}_{1}}\]
Notice carefully that we have removed three diagonals that are
Same 7 possibility is there for other 10 points also
So, we can write total \[7\times 10=70\] possibilities of making a diagonal in a decagon
But notice carefully that we have counted each diagonal twice
For example, if I counted 7 diagonals for point \[{{A}_{1}}\] which includes diagonal with point
\[{{C}_{1}},{{D}_{1}},{{E}_{1}},{{F}_{1}},{{G}_{1}},{{H}_{1}},{{I}_{1}}\]
Now when counting diagonals from these point \[{{C}_{1}},{{D}_{1}},{{E}_{1}},{{F}_{1}},{{G}_{1}},{{H}_{1}},{{I}_{1}}\] , we have calculated diagonals with\[{{A}_{1}}\] again , in other words we have counted diagonal \[{{A}_{1}}{{C}_{1}}\] and \[{{C}_{1}}{{A}_{1}}\] as different diagonals so we have to exclude those cases .
As we have counted each diagonal twice so we can just divide equation \[7\times 10=70\] with 2
\[\dfrac{70}{2}=35\]
Hence total number of diagonals in a decagon are 35

Note: Most of the times while solving permutation problems , we might have counted same case twice as we have counted in this problem also , so be careful about that.There is a shortcut formula for finding diagonal of any polygon which is \[\dfrac{n(n-3)}{2}\] ,Where n is the number of sides, so in this case \[n=10\] , total diagonal will be. \[\dfrac{10(10-3)}{2}=\dfrac{70}{2}=35\]