Questions & Answers
Question
AnswersFind the minimum value of \[\cos \theta + \cos 2\theta \]for all real value of \[\theta \]
Answer
Verified128.1k+ views
Hint: The cosine function is a periodic function which is very important in trigonometry. The simplest way to understand the cosine function is to use the unit circle. For a given angle measure (-) draw a unit circle on the coordinate plane and draw the angle centered at the origin with one side as the positive \[x - axiz\] the \[x - \] coordinate of the point where the other side of the angle intersects the circle is \[\cos (\theta )\], and the y coordinate is \[\sin (\theta )\]
The amplitude of a wave is basically a measure of its height. Because that height is constantly changing amplitude can be different form moment to moment. If the wave has a regular up and down shape, like a cosine, sine wave. The amplitude is defined as the fact act distance the wave gets from its center.
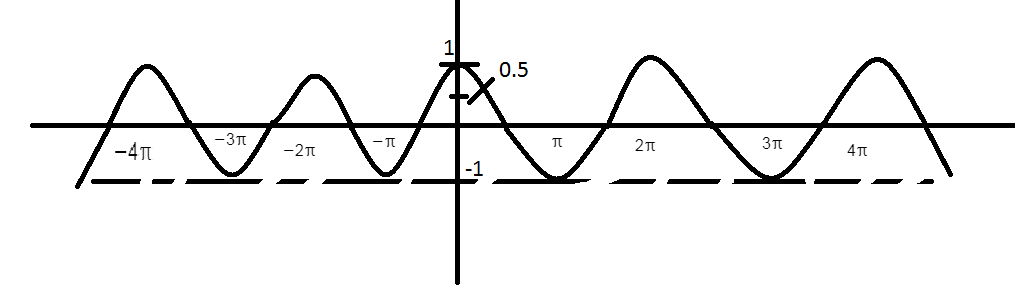
Which shows that
Max value of \[\cos \,\,\,\,\,\, + 1\]
Min value of \[\cos \,\,\,\,\,\, - 1\]
Complete step by step answer:
Given function is
\[ = \cos 2\theta + \cos \theta \]
\[ = 2{\cos ^2}\theta - 1 + \cos \theta \] \[\left[ {\cos 2\theta - 2{{\cos }^2}\theta - 1} \right]\]
\[ = {\cos ^2}\theta - \dfrac{1}{2}\cos \theta - \dfrac{1}{2}\]\[\left[ {dividing\;by\,2} \right]\]
\[ = ({\cos ^2}\theta + \dfrac{1}{2}\cos \theta + \dfrac{1}{{16}}) - \dfrac{1}{{16}} - \dfrac{1}{2}\] \[\left[ {For\,factorize\,add\& substract\,\dfrac{1}{{16}}} \right]\]
\[ = {(\cos \theta + \dfrac{1}{2})^2} - (\dfrac{{1 + 8}}{{16}})\] \[\left[ {Making\,the\,whole\,square} \right]\]
\[ = {(\cos \theta + \dfrac{1}{4})^2} - (\dfrac{9}{{16}})\]
Now for minimum value if \[\cos \theta = 0\]
i.e.\[ = \dfrac{{ - 9}}{{16}}\]
Required minimum value of \[\cos \theta + \cos 2\theta \] for all real values of \[\theta \] is \[ = \dfrac{{ - 9}}{{16}}\]
\[(\cos + \dfrac{1}{2})\dfrac{1}{2}O\]
\[\cos \theta = \dfrac{1}{2}\]
Note: If we take negative value of \[\cos \theta \] because it’s a square so at last it become positive.
Minimum value of \[\cos \theta \] is -1 when \[\theta = {180^0}\] Maximum value \[\cos \theta \] 1 when\[\theta \] is \[O,360\] Min-Max table.
The amplitude of a wave is basically a measure of its height. Because that height is constantly changing amplitude can be different form moment to moment. If the wave has a regular up and down shape, like a cosine, sine wave. The amplitude is defined as the fact act distance the wave gets from its center.
Which shows that
Max value of \[\cos \,\,\,\,\,\, + 1\]
Min value of \[\cos \,\,\,\,\,\, - 1\]
Complete step by step answer:
Given function is
\[ = \cos 2\theta + \cos \theta \]
\[ = 2{\cos ^2}\theta - 1 + \cos \theta \] \[\left[ {\cos 2\theta - 2{{\cos }^2}\theta - 1} \right]\]
\[ = {\cos ^2}\theta - \dfrac{1}{2}\cos \theta - \dfrac{1}{2}\]\[\left[ {dividing\;by\,2} \right]\]
\[ = ({\cos ^2}\theta + \dfrac{1}{2}\cos \theta + \dfrac{1}{{16}}) - \dfrac{1}{{16}} - \dfrac{1}{2}\] \[\left[ {For\,factorize\,add\& substract\,\dfrac{1}{{16}}} \right]\]
\[ = {(\cos \theta + \dfrac{1}{2})^2} - (\dfrac{{1 + 8}}{{16}})\] \[\left[ {Making\,the\,whole\,square} \right]\]
\[ = {(\cos \theta + \dfrac{1}{4})^2} - (\dfrac{9}{{16}})\]
Now for minimum value if \[\cos \theta = 0\]
i.e.\[ = \dfrac{{ - 9}}{{16}}\]
Required minimum value of \[\cos \theta + \cos 2\theta \] for all real values of \[\theta \] is \[ = \dfrac{{ - 9}}{{16}}\]
\[(\cos + \dfrac{1}{2})\dfrac{1}{2}O\]
\[\cos \theta = \dfrac{1}{2}\]
Note: If we take negative value of \[\cos \theta \] because it’s a square so at last it become positive.
Minimum value of \[\cos \theta \] is -1 when \[\theta = {180^0}\] Maximum value \[\cos \theta \] 1 when\[\theta \] is \[O,360\] Min-Max table.