Question

Find the measure of an exterior angle at the base of an isosceles triangle measuring ${{78}^{\circ }}$.
A. ${{100}^{\circ }}$
B. ${{101}^{\circ }}$
C. ${{102}^{\circ }}$
D. ${{103}^{\circ }}$

Answer 1

Hint: For solving this question you should know about the general properties of triangles. According to the properties of a triangle the sum of angles at a point or corner or where two sides are matching with one another is always ${{180}^{\circ }}$ and this is the addition of two angles, one is interior angle and the other is exterior angle.

Complete step by step answer:
According to our question we have to find the measure of an exterior angle at the base of an isosceles triangle measuring ${{78}^{\circ }}$. As we know that a triangle has a total sum of all interior angles as ${{180}^{\circ }}$ always. And the triangle can be of any type but this sum remains the same. And at any joining point of two sides if we increase to any one side till infinite or any finite length then there are two angles, one is the angle which is inside the triangle, that is the interior angle and the second is the angle which is between the increased side and the not increased side, and this is outside the triangle and it is known as the exterior angle. The submission of both these angles remains the same and that is ${{180}^{\circ }}$. So, if we see our question, then:

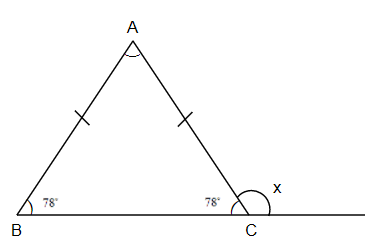
Base angles of the isosceles triangle are equal.
$\therefore \angle B=\angle C={{78}^{\circ }}$
Now $x+\angle C={{180}^{\circ }}$ (angles made on straight line)
$\begin{align}
  & x={{180}^{\circ }}-{{78}^{\circ }} \\
 & \Rightarrow x={{102}^{\circ }} \\
\end{align}$
So, the exterior angle is ${{102}^{\circ }}$

So, the correct answer is “Option C”.

Note: While solving this type of questions you have to be careful while selecting the exterior and interior angle of a triangle at any point. And the submission of angle at a point of straight line is always fixed and that is ${{180}^{\circ }}$. And the base angles of isosceles triangles always remain equal.