Question

Find the length of the perpendicular from the point \[\left( {3,2,1} \right)\]to the line\[\dfrac{{x - 7}}{{ - 2}} = \dfrac{{y - 7}}{2} = \dfrac{{z - 6}}{3}\].

Answer 1

Hint: A line is said to be perpendicular to the other line if the angle between them is\[{90^ \circ }\], a straight line is defined as a line that does not have any curve or the angle made between any two points on the line is always 180 degrees.
In this question, the length of the perpendicular is needed to be determined from the \[\left( {3,2,1} \right)\]to the line\[\dfrac{{x - 7}}{{ - 2}} = \dfrac{{y - 7}}{2} = \dfrac{{z - 6}}{3}\] for which consider a point M on the line which makes an angle of 90 degrees with the given point and use the concept that the sum of the product of the direction ratio of both the line will be equal to 0.


Complete step by step answer:
 Let M be a point on the given line where the line from point \[P\left( {3,2,1} \right)\]is perpendicular

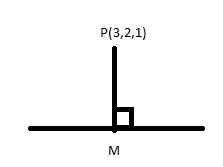
Consider
\[\dfrac{{x - 7}}{{ - 2}} = \dfrac{{y - 7}}{2} = \dfrac{{z - 6}}{3} = h\]
Hence we can write
\[
  \dfrac{{x - 7}}{{ - 2}} = h \\
  x - 7 = - 2h \\
  x = 7 - 2h - - - (i) \\
 \]
\[
  \dfrac{{y - 7}}{2} = h \\
  y - 7 = 2h \\
  y = 7 + 2h - - - (ii) \\
 \]
\[
  \dfrac{{z - 6}}{3} = h \\
  z - 6 = 3h \\
  z = 6 + 3h - - - (iii) \\
 \]
So the coordinate of point
\[M\left( {x,y,z} \right) = M\left( {7 - 2h,7 + 2h,6 + 3h} \right)\]
Now the direction ratio of the line PM will be equal to:
\[
  \left( {7 - 2h - 3,7 + 2h - 2,6 + 3h - 1} \right) \\
  \left( {4 - 2h,5 + 2h,5 + 3h} \right) \\
 \]
The direction ratio of the given line on which PM is perpendicular is given as\[\left( { - 2,2,3} \right)\],
Since line PM is perpendicular to the given line so the sum of the product of the direction ratio of both the line will be equal to 0, hence we can write
\[
  \left( {4 - 2h} \right)\left( { - 2} \right) + \left( {5 + 2h} \right)\left( 2 \right) + \left( {5 + 3h} \right)\left( 3 \right) = 0 \\
   - 8 + 4h + 10 + 4h + 15 + 9h = 0 \\
  17h = - 17 \\
  h = - \dfrac{{17}}{{17}} \\
  h = - 1 \\
 \]
Now put the value of \[h\] in coordinate point of M
\[M\left( {7 - 2h,7 + 2h,6 + 3h} \right) = \left( {9,5,3} \right)\]
Hence the length of the perpendicular line PM will be
\[
  PM = \sqrt {{{\left( {9 - 3} \right)}^2} + {{\left( {5 - 2} \right)}^2} + {{\left( {3 - 1} \right)}^2}} \\
   = \sqrt {{6^2} + {3^2} + {2^2}} \\
   = \sqrt {36 + 9 + 4} \\
   = \sqrt {49} \\
   = 7 \\
 \]

Note:
 In two dimensional plane, a line is represented by the general equation\[y = mx + c\], where m is the slope of the line in that 2-d plane but in the case of a three-dimensional plane a straight line is defined as the intersection of two planes which is the equation of two planes together given as \[{a_1}x + {b_1}y + {c_1}z + {d_1} = 0,\]\[{a_2}x + {b_2}y + {c_2}z + {d_2} = 0\].