Question

Find the length of the bisector of angle A in a triangle ABC.

A. \[\dfrac{{2bc\sin (A/2)}}{{b + c}}\]
B.$\dfrac{{2bc\cos (A/2)}}{{b + c}}$
C. $\dfrac{{abc}}{{2R(b + c)}}\csc (A/2)$
D. $\dfrac{{4\Delta }}{{b + c}}\csc (A/2)$

Answer 1

Hint: Here the properties of bisector are the only information which we use to reach the solution, which are as follows:
* Bisector of an angle A is defined to be the line cutting off A into equal halves which meets the
   opposite side. In the below figure, AD is the bisector of angle A. Thus it divides angle A into 2 equal
   halves and meets the opposite side BC.
                              

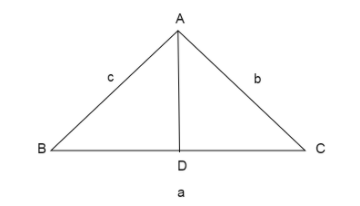
* Bisector of an angle of a triangle divides the opposite side in the ratio of the sides containing the angle.
   Implies point D divides BC into the ratio of sides containing angle A which are AC and AB. Thus
   $\dfrac{{BD}}{{DC}} = \dfrac{{AC}}{{AB}}$

* Sine rule: Ratios of a side to corresponding opposite angles are equal. $\dfrac{{AB}}{{\sin C}} = \dfrac{{AC}}{{\sin B}} = \dfrac{{BC}}{{\sin A}}$

Complete step-by-step answer:
We start with bisector AD and develop its relation with the interior angles.
Sine rules on the triangle ABD gives the result: $\dfrac{{AD}}{{\sin B}} = \dfrac{{BD}}{{\sin (A/2)}}$
From the property of bisector and sine rule, $BD = \dfrac{c}{{b + c}}a$
$AD = \dfrac{{ca}}{{b + c}}\dfrac{{\sin B}}{{\sin (A/2)}}$
Multiplying numerator and denominator by $2\cos (A/2)$, for simplifying the equation to shorter terms.
$AD = \dfrac{{ca.\sin B.2\cos (A/2)}}{{(b + c)\sin (A/2).2\cos (A/2)}}$
Using the formula $\sin (2\theta ) = 2\sin \theta \cos \theta $ ,
$AD = 2.\dfrac{{ca.\sin B.\cos (A/2)}}{{(b + c)\sin A}}$
Using sine rule: $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}}$ we get,
$
  AD = 2.\dfrac{{cb\sin B\cos (A/2)}}{{(b + c)\sin B}} \\
   = \dfrac{{2cb\cos (A/2)}}{{b + c}} \\
$
From the property of bisector and sine rule,
$AD = \dfrac{{2bc}}{{b + c}}\dfrac{{\cos (A/2)\sin (A/2)}}{{\sin (A/2)}}$
Simplifying,
$AD = \dfrac{{bc}}{{\sin (A/2)}}\dfrac{{\sin A}}{{\sin (A/2)}}$
Using $\sin A = \dfrac{a}{{2R}}$ , $\dfrac{1}{{\sin (A/2)}} = \csc (A/2)$ we get,
$AD = \dfrac{{abc}}{{2R(b + c)}}\csc (A/2)$
As $R = \dfrac{{abc}}{{4\Delta }}$
$AD = \dfrac{{abc.4\Delta }}{{2abc(b + c)}}\csc (A/2)$
Simplifying,
$AD = \dfrac{{2\Delta }}{{b + c}}\csc (A/2)$

So, the correct answer is “Option B” and “Option C”.

Note: Students are likely to make mistakes while substituting the sides using the sine formula, always keep in mind the angle opposite to the side comes in denominator along with the side in the numerator. Making the rearrangements of terms according to our motive is to be done properly for a quick solution. Multiplying and dividing by needed trigonometric terms can cut short the solution into simpler form lines.