Question

Find the lateral surface area and total surface area of an equilateral triangle-based prism with height 8 cm and base 4 cm.

Answer 1

Hint: First of all, draw the diagram of the equilateral triangle-based prism to have a clear idea of what we have to find. Then use the formula for finding L.S.A and T.S.A of the equilateral triangle-based prism.

Complete step-by-step solution:
Given that the base of the prism is an equilateral triangle with side 4 cm as shown in the given figure:

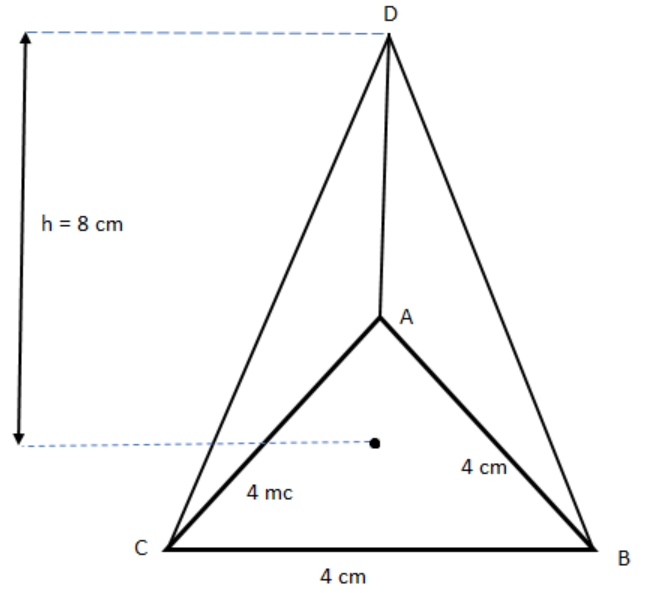
Let \[p\] be the perimeter of the base of the prism i.e., the perimeter of equilateral \[\Delta ABC\].
So, \[p = 4 + 4 + 4 = 12{\text{ cm}}\]
Given height of the prism \[h = 8\;{\text{cm}}\]
We know that the lateral surface area of the triangle-based prism is given by \[p \times h\] where \[p\] is the perimeter of the base triangle and \[h\] is the height of the prism.
Therefore, L.S.A of the prism \[ = p \times h = 12 \times 8 = 96{\text{ c}}{{\text{m}}^2}\]
Now, consider the area of equilateral \[\Delta ABC\].
We know that the area of the equilateral triangle with side \[a\] is given by \[\dfrac{{{a^2}}}{4}\].
So, area of \[\Delta ABC = \dfrac{{\sqrt 3 {{\left( 4 \right)}^2}}}{4} = 4\sqrt 3 \]
We know that the total surface area of the triangle based prism with base area \[A\], perimeter \[p\] and \[h\] is the height of the prism is given by \[2 \times A + p \times h\].
Therefore, the total surface area of the prism \[ = 2 \times 4\sqrt 3 + 12 \times 8\]
\[
  = 8\sqrt 3 + 96 \\
   = 8\left( {1.73} \right) + 96 \\
   = 13.84 + 96 \\
   = 109.84{\text{ c}}{{\text{m}}^2} \]
Thus, the L.S.A of the prism is \[96{\text{ c}}{{\text{m}}^2}\] and the T.S.A of the prism is \[{\text{109}}{\text{.84 c}}{{\text{m}}^2}\].

Note: The lateral surface area of the triangle-based prism is given by \[p \times h\] where \[p\] is the perimeter of the base triangle and \[h\] is the height of the prism. The total surface area of the triangle based prism with base area \[A\], perimeter \[p\] and \[h\] is the height of the prism is given by \[2 \times A + p \times h\].