Questions & Answers
Question
Answers
Related Questions
Find the intervals of concavity and the points of inflexion of the function
\[f\left( x \right)={{\left( x-1 \right)}^{\dfrac{1}{3}}}\]
Answer
![Verified]()
Verified
Verified
Hint: Double differentiate the given f(x) and find whether it is positive or negative. When f''(x) > 0, then the graph of f (x) is concave upwards and when f''(x )< 0, then the graph of f (x) is concave downwards. Also we will get the inflexion point at x where f'' (x) = 0 or does not exist.
Complete step-by-step answer:
Here we have to find the intervals of concavity and points of inflexion of function
\[f\left( x \right)={{\left( x-1 \right)}^{\dfrac{1}{3}}}\]
We know that if double derivative of function which is \[{{f}^{''}}\left( x \right)>0\text{ }\forall \text{ }x\in \left( a,b \right)\], then the graph of f (x) is concave upwards in (a, b).
Similarly, if \[{{f}^{''}}\left( x \right)<0\text{ }\forall \text{ }x\in \left( a,b \right)\], then the graph of f (x) is concave downwards in (a, b).
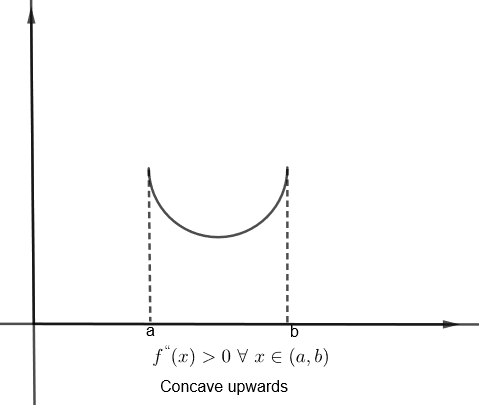
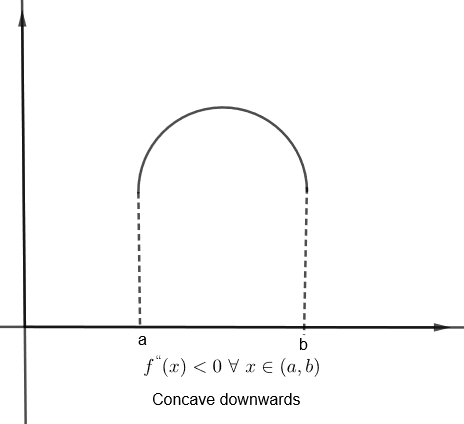
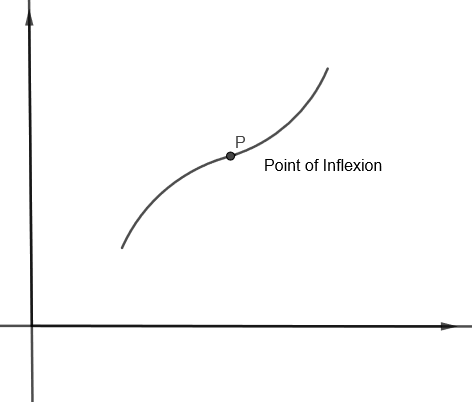
The point at which concavity of graph changes, i.e. \[\dfrac{{{d}^{2}}x}{d{{y}^{2}}}=0\] or does not exist is the point of inflexion.
The sign of \[\dfrac{{{d}^{2}}x}{d{{y}^{2}}}\] changes about the point of inflexion.
Now, we can take
\[f\left( x \right)={{\left( x-1 \right)}^{\dfrac{1}{3}}}\]
We know that,
\[\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}\]
Now, we will differentiate f (x). We get,
\[{{f}^{'}}\left( x \right)=\dfrac{1}{3}{{\left( x-1 \right)}^{\dfrac{1}{3}-1}}\]
\[{{f}^{'}}\left( x \right)=\dfrac{1}{3}{{\left( x-1 \right)}^{\dfrac{-2}{3}}}\]
Now, again we will differentiate the above equation. We get,
\[{{f}^{''}}\left( x \right)=\dfrac{1}{3}\left( \dfrac{-2}{3} \right){{\left( x-1 \right)}^{\dfrac{-2}{3}-1}}\]
\[{{f}^{''}}\left( x \right)=\dfrac{-2}{9}{{\left( x-1 \right)}^{\dfrac{-5}{3}}}\]
Or, \[{{f}^{''}}\left( x \right)=\dfrac{-2}{9{{\left( x-1 \right)}^{\dfrac{5}{3}}}}\]
We know that the point of inflexion is a point where \[{{f}^{''}}\left( x \right)=0\] or does not exist. It changes its sign.
As we can see that \[{{f}^{''}}\left( x \right)\] cannot be zero but \[{{f}^{''}}\left( x \right)\] will not exist at x = 1 as (x – 1) which is in the denominator will become zero at x = 1.
Now, for x > 1, (x – 1) would be greater than zero. So,
\[{{\left( x-1 \right)}^{\dfrac{5}{3}}}>0\]
Therefore,
\[{{f}^{''}}\left( x \right)=\dfrac{-2}{9{{\left( x-1 \right)}^{\dfrac{5}{3}}}}<0\]
As for any value of x, say x = 2 in this case, we would get the value of \[{{f}^{''}}\left( x \right)\text{ as }\dfrac{-2}{9}\].
Now, for x < 1, (x – 1) would be less than zero. So,
\[{{\left( x-1 \right)}^{\dfrac{5}{3}}}<0\]
Therefore,
\[{{f}^{''}}\left( x \right)=\dfrac{-2}{9{{\left( x-1 \right)}^{\dfrac{5}{3}}}}>0\]
As for any value of x, say x = 0 in this case, we would get the value of \[{{f}^{''}}\left( x \right)\text{ as }\dfrac{2}{9}\].
Therefore, as f”(x) does not exist at x = 1, and f”(x) is positive for x < 1 and negative for x > 1, that is f (x) changes its sign about the point x = 1. Therefore, x = 1 is inflexion point.
As we have proved that f”(x) > 0 for x < 1
Therefore, f(x) is concave upwards for \[\left( -\infty ,1 \right)\]
As we have proved that f”(x) < 0 for x > 1
Therefore, f(x) is concave downwards for \[\left( 1,\infty \right)\]
Note: Students should always check if the function is changing its sign at an inflexion point and not only rely upon \[\dfrac{{{d}^{2}}y}{d{{x}^{2}}}=0\] or does not exist for finding the inflexion point.
Complete step-by-step answer:
Here we have to find the intervals of concavity and points of inflexion of function
\[f\left( x \right)={{\left( x-1 \right)}^{\dfrac{1}{3}}}\]
We know that if double derivative of function which is \[{{f}^{''}}\left( x \right)>0\text{ }\forall \text{ }x\in \left( a,b \right)\], then the graph of f (x) is concave upwards in (a, b).
Similarly, if \[{{f}^{''}}\left( x \right)<0\text{ }\forall \text{ }x\in \left( a,b \right)\], then the graph of f (x) is concave downwards in (a, b).
The point at which concavity of graph changes, i.e. \[\dfrac{{{d}^{2}}x}{d{{y}^{2}}}=0\] or does not exist is the point of inflexion.
The sign of \[\dfrac{{{d}^{2}}x}{d{{y}^{2}}}\] changes about the point of inflexion.
Now, we can take
\[f\left( x \right)={{\left( x-1 \right)}^{\dfrac{1}{3}}}\]
We know that,
\[\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}\]
Now, we will differentiate f (x). We get,
\[{{f}^{'}}\left( x \right)=\dfrac{1}{3}{{\left( x-1 \right)}^{\dfrac{1}{3}-1}}\]
\[{{f}^{'}}\left( x \right)=\dfrac{1}{3}{{\left( x-1 \right)}^{\dfrac{-2}{3}}}\]
Now, again we will differentiate the above equation. We get,
\[{{f}^{''}}\left( x \right)=\dfrac{1}{3}\left( \dfrac{-2}{3} \right){{\left( x-1 \right)}^{\dfrac{-2}{3}-1}}\]
\[{{f}^{''}}\left( x \right)=\dfrac{-2}{9}{{\left( x-1 \right)}^{\dfrac{-5}{3}}}\]
Or, \[{{f}^{''}}\left( x \right)=\dfrac{-2}{9{{\left( x-1 \right)}^{\dfrac{5}{3}}}}\]
We know that the point of inflexion is a point where \[{{f}^{''}}\left( x \right)=0\] or does not exist. It changes its sign.
As we can see that \[{{f}^{''}}\left( x \right)\] cannot be zero but \[{{f}^{''}}\left( x \right)\] will not exist at x = 1 as (x – 1) which is in the denominator will become zero at x = 1.
Now, for x > 1, (x – 1) would be greater than zero. So,
\[{{\left( x-1 \right)}^{\dfrac{5}{3}}}>0\]
Therefore,
\[{{f}^{''}}\left( x \right)=\dfrac{-2}{9{{\left( x-1 \right)}^{\dfrac{5}{3}}}}<0\]
As for any value of x, say x = 2 in this case, we would get the value of \[{{f}^{''}}\left( x \right)\text{ as }\dfrac{-2}{9}\].
Now, for x < 1, (x – 1) would be less than zero. So,
\[{{\left( x-1 \right)}^{\dfrac{5}{3}}}<0\]
Therefore,
\[{{f}^{''}}\left( x \right)=\dfrac{-2}{9{{\left( x-1 \right)}^{\dfrac{5}{3}}}}>0\]
As for any value of x, say x = 0 in this case, we would get the value of \[{{f}^{''}}\left( x \right)\text{ as }\dfrac{2}{9}\].
Therefore, as f”(x) does not exist at x = 1, and f”(x) is positive for x < 1 and negative for x > 1, that is f (x) changes its sign about the point x = 1. Therefore, x = 1 is inflexion point.
As we have proved that f”(x) > 0 for x < 1
Therefore, f(x) is concave upwards for \[\left( -\infty ,1 \right)\]
As we have proved that f”(x) < 0 for x > 1
Therefore, f(x) is concave downwards for \[\left( 1,\infty \right)\]
Note: Students should always check if the function is changing its sign at an inflexion point and not only rely upon \[\dfrac{{{d}^{2}}y}{d{{x}^{2}}}=0\] or does not exist for finding the inflexion point.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
-
LIVECourses
-
Crash Courses 2021
-
Vedantu Pro
-
Vedantu Assist
-
Class 12
-
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
JEE Main & Advanced 2023
-
-
NEET
-
NEET 2021
-
NEET 2022
-
NEET 2023
-
-
NDA
-
CBSE
-
Commerce
-
Class 11
-
Class 12
-
-
ICSE
-
Maharashtra Board
-
Micro Courses
-
-
Reading & Spoken English -
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
