Question

Find the height of the tree when it if found that on walking away from it 20m, in a horizontal line through its base, the elevation of the top changes from ${{30}^{\circ }}$ to ${{60}^{\circ }}$.

Answer 1

Hint: To solve this question we need to know the concept of height and distance which is an application of trigonometry. To solve the problem the first step is to draw a diagram which exhibits the above condition. The next step is to use the trigonometric function to find the value of the height of the tree.

Complete step-by-step solution:
The question ask us to find the value of height of the tree if on walking away $20m$ from the tree in horizontal line the elevation of the top changes from ${{30}^{\circ }}$ to ${{60}^{\circ }}$. We will be solving this question. We need to take the help of the diagram. The diagram is given below. In the diagram $AB$ is the height of the tree, which we are told to find. $DC$is the distance covered in horizontal lines which is $20m$.

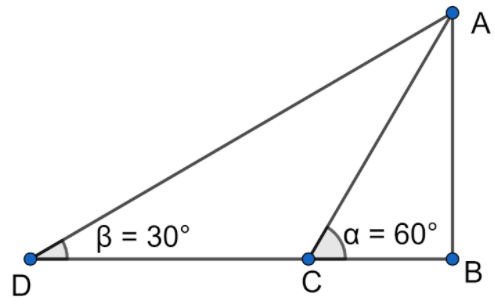
After analysing the above diagram we will apply the trigonometric function to find the height. Let us consider the height of the tree which is indicated in the diagram as $AB$ is $h$, and the value of $DC=20m$ ,$\angle ADB={{30}^{\circ }}$ and $\angle ACB={{60}^{\circ }}$.
To solve we will be first considering the $\vartriangle ABC$,
On applying the trigonometric function $\tan $ we get:
$\Rightarrow \tan {{60}^{\circ }}=\sqrt{3}$
Since we know that the trigonometric function$\tan $is the ratio of height and the base. So in this case it is:
$\Rightarrow \tan {{60}^{\circ }}=\dfrac{AB}{BC}$
\[\Rightarrow \sqrt{3}=\dfrac{AB}{BC}\]
\[\Rightarrow \sqrt{3}=\dfrac{h}{BC}\]
On cross multiplying we get:
\[\Rightarrow BC=\dfrac{h}{\sqrt{3}}\]
The next step is to consider the triangle $\vartriangle ABD$
On applying the trigonometric function $\tan $ again we get:
$\Rightarrow \tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$
Since we know that $DB$ could be written as the sum of the two line segments which are $DC$ and $CB$,$DB=DC+CB$ . So in this case it is:
$\Rightarrow \tan {{30}^{\circ }}=\dfrac{h}{20+BC}$
\[\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h}{20+BC}\]
On cross multiplying we get:
\[\Rightarrow BC+20=\sqrt{3}h\]
On substituting the value of $BC$ in the above equation we get:
\[\Rightarrow \dfrac{h}{\sqrt{3}}+20=\sqrt{3}h\]
\[\Rightarrow 20=\sqrt{3}h-\dfrac{h}{\sqrt{3}}\]
We will take “h” as common to find its value:
\[\Rightarrow 20=h\left( \sqrt{3}-\dfrac{1}{\sqrt{3}} \right)\]
\[\Rightarrow h\left( 1.154 \right)=20\]
On dividing the R.H.S and the L.H.S function by \[1.154\]we get:
\[\Rightarrow \dfrac{20}{1.154}=h\]
\[\Rightarrow h=17.32\]
$\therefore $ The value of the height of the tree is \[17.32m\].

Note: To solve this type of question we need to analyse the problem and check which trigonometric function will be most applicable to find the value of the unknown. For example, as per the values given to us in the question the trigonometric function which was best was $\tan x$ which has been used in the problem.