Question

Find the equation of a line whose x intercept is 5 and y intercept is 2.

Answer 1

Hint: This question is based on a straight line in a plane.
So first we will learn some topics about straight lines.
1. Straight line – Shortest distance between two points is called a straight line.

Here line AB is, line joining points A and B with coordinates $A({x_1},{y_1})$ and $B({x_2},{y_2})$.
2. Slope of a line - $\tan \theta $ is called the slope or gradient of line. If $\theta $ is the inclination of a line AB,
Then slope, $m = \tan \theta $

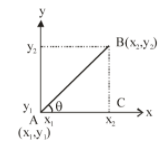
We know that slope, $m = \tan \theta $
So, from above diagram –
$m = \dfrac{{perpendicular}}{{base}}$
$m = \dfrac{{BC}}{{AC}} = \dfrac{{({y_2} - {y_1})}}{{({x_2} - {x_1})}}$
So, $m = \tan \theta = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
3. General equation of line – The general equation of a straight line is $ax + bx = c$
Where a, b and c are constants

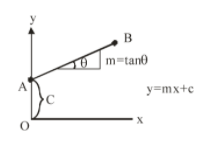
4. Various forms of equations of line –
(i) Slope-point form : When a point online is given and slope, m is known then equation will be $y - {y_0} = m(x - {x_0})$
(ii) Two point form : Equation of the line passing through two given points $A({x_1},{y_1})$ and $B({x_2},{y_2})$ is $(y - {y_1}) = \left( {\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right)(x - {x_1})$
(iii) Slope-intercept form : If the slope m and the y intercept are known. Then equation will be $y = mx + c$
Where, m is the slope of line, $y = c$ is the value where the line cuts the y-axis. This number c is called the intercept on the y-axis.
(iv) Intercept form : $\dfrac{x}{a} + \dfrac{y}{b} = 1$ where a is intercept on x-axis and b is intercept on y-axis.

Complete step by step solution: It is given that,
Intercept of x, $a = 5$
Intercept of y, $b = 2$
When both the intercepts are given then, the equation of line will be in the form of “intercept form”.
So, substituting the values in equation for intercept of line
$\dfrac{x}{a} + \dfrac{y}{b} = 1$
We get $\dfrac{x}{5} + \dfrac{y}{2} = 1$
or we can arrange the equation in the form of general equation of line
$2x + 5y = 10$
$2x + 5y - 10 = 0$
In slope intercept form $(i.e.,y = mx + c)$
$5y = 10 - 2x$
$y = \dfrac{{10}}{5} - \dfrac{{2x}}{5}$
$y = \dfrac{{ - 2x}}{5} + 2$
Therefore, equation of a line whose x intercept is 5 and y intercept is 2 is $2x + 5y - 10 = 0$

Note: 1. Generally students make mistakes while substituting values of intercepts. In formula, intercepts are a and b but most of them put them in the place of x and y.
2. Every time we don’t need to give answers in various forms of lines like we do in the above question.
Just finish the calculation after getting general form i.e., $ax + by - c = 0$. No need to find the equations in the forms when it is not asked in question. We just did the same to give better understanding towards the question.