
Find the distance covered by the wheel of a bus in 1000 revolutions if the diameter of the wheel is 56 cm.
Answer
503.1k+ views
Hint: Assume the given diameter of the wheel as d. Find the radius (r) of the wheel by using the relation d = 2r. Now, consider that the distance covered by the wheel in one revolution will be equal to the circumference of the wheel and find the distance covered in one revolution using the formula $C=2\pi r$ where C = circumference. Multiply both the sides with 1000 to get the answer.
Complete step by step answer:
Here we have been asked to find the distance covered by the wheel of a bus which takes 1000 revolutions and whose diameter is 56 cm. First let us find the radius of the wheel.
Now, we know that the diameter (d) of a circle is twice its radius (r) so using the relation d = 2r we get,
$\Rightarrow r=\dfrac{d}{2}$
Substituting the value of d = 56 cm we get,
$\Rightarrow r=\dfrac{56}{2}$
$\Rightarrow $ r = 28 cm
Now, in one revolution the wheel will cover a distance equal to its circumference, so applying the formula for the circumference (C) of a circle given as $C=2\pi r$ we get,
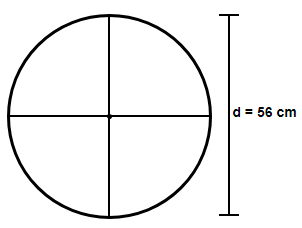
$\Rightarrow $ Distance covered in 1 revolution = $2\times \dfrac{22}{7}\times 28$
$\Rightarrow $ Distance covered in 1 revolution = 176 cm
Multiplying both the sides with 1000 we get,
$\Rightarrow $ Distance covered in 1000 revolution = 176000 cm
We know that 100 cm = 1m and 1000m = 1km so using these two relations we get,
$\therefore $ Distance covered in 1000 revolution = 1.76 km
Hence, the distance travelled by the wheel in 1000 revolutions is 1.76 km.
Note: Note that it is not necessary to convert the diameter of the wheel into the radius as you can remember the direct relation between the circumference and diameter given as $C=\pi d$. Although you must remember the relation d = 2r. We have taken the value of $\pi =\dfrac{22}{7}$ only to reduce our calculations because we can see that 28 can easily be cancelled by 7 present in the denominator.
Complete step by step answer:
Here we have been asked to find the distance covered by the wheel of a bus which takes 1000 revolutions and whose diameter is 56 cm. First let us find the radius of the wheel.
Now, we know that the diameter (d) of a circle is twice its radius (r) so using the relation d = 2r we get,
$\Rightarrow r=\dfrac{d}{2}$
Substituting the value of d = 56 cm we get,
$\Rightarrow r=\dfrac{56}{2}$
$\Rightarrow $ r = 28 cm
Now, in one revolution the wheel will cover a distance equal to its circumference, so applying the formula for the circumference (C) of a circle given as $C=2\pi r$ we get,
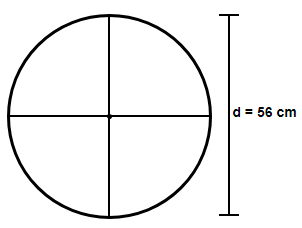
$\Rightarrow $ Distance covered in 1 revolution = $2\times \dfrac{22}{7}\times 28$
$\Rightarrow $ Distance covered in 1 revolution = 176 cm
Multiplying both the sides with 1000 we get,
$\Rightarrow $ Distance covered in 1000 revolution = 176000 cm
We know that 100 cm = 1m and 1000m = 1km so using these two relations we get,
$\therefore $ Distance covered in 1000 revolution = 1.76 km
Hence, the distance travelled by the wheel in 1000 revolutions is 1.76 km.
Note: Note that it is not necessary to convert the diameter of the wheel into the radius as you can remember the direct relation between the circumference and diameter given as $C=\pi d$. Although you must remember the relation d = 2r. We have taken the value of $\pi =\dfrac{22}{7}$ only to reduce our calculations because we can see that 28 can easily be cancelled by 7 present in the denominator.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




